Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Circuitos Trifásicos Desequilibrados

Ver Teoria
Exercício 41235678910

Enunciado

Considere o sistema triângulo-triângulo mostrado na figura abaixo. Adote Z 1 = 8 + j 6   Ω , Z 2 = 4,2 - j 2,2   Ω e Z 3 = 10   Ω .

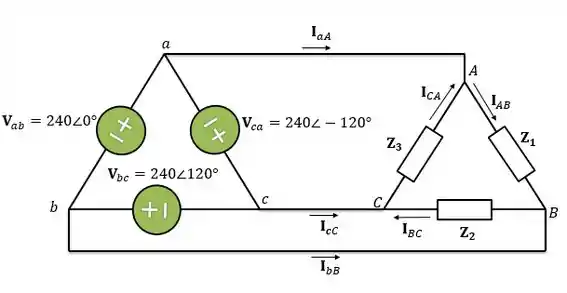
( a ) Determine as correntes de fase I A B , I B C e I C A

( b ) Calcule as correntes de linha I a A , I b B e I c C

Passo 1

O circuito acima é desbalanceado porque as impedâncias possuem valores diferentes. Logo, para calcularmos as correntes de fase, vamos utilizar a Lei de Ohm.

Calculando I A B :

I A B = V a b Z 1 = 240 ∠ 0 ° 8 + j 6   = 240 ∠ 0 ° 10 ∠ 36,9 °

I A B = 24 ∠ - 36,9 °   A

I A B = 19,2 - j 14,4   A

Calculando I B C :

I B C = V b c Z 2 = 240 ∠ 120 ° 4,2 - j 2,2     = 240 ∠ 120 ° 4,74 ∠ - 27,6 °

I B C = 50,62 ∠ 147,64 °   A

I B C = - 42,76 + j 27,1   A

Calculando I C A :

I C A = V c a Z 3 = 240 ∠ - 120 ° 10    

I C A = 24 ∠ - 120 °   A

I C A = - 12 - j 20,8   A

Passo 2

Agora, calculando as correntes de linha, utilizaremos a Lei dos Nós.

Para o nó A :

I a A + I C A = I A B

I a A = I A B - I C A

I a A = 19,2 - j 14,4 - - 12 - j 20,8

I a A = 31,2 + j 6,4   A

Para o nó B :

I b B + I A B = I B C

I b B = I B C - I A B

I b B = - 42,76 + j 27,1 - 19,2 - j 14,4

I b B = - 61,96 + j 41,5   A

Para o nó C :

I c C + I B C = I C A

I c C = I C A - I B C

I c C = - 12 - j 20,8   - - 42,76 + j 27,1

I c C = 30,76 - j 47,9   A

Resposta

a   I A B = 19,2 - j 14,4   A

                          I B C = - 42,76 + j 27,1   A

            I C A = - 12 - j 20,8   A

b     I a A = 31,2 + j 6,4   A

                              I b B = - 61,96 + j 41,5   A

                    I c C = 30,76 - j 47,9   A

Exercícios de Livros Relacionados

Para o circuito mostrado na Figura P11.20, determinea) as correntes de fase I A B ,I B CeI C A ,b) as correntes de linha I a A ,I b BeI c C , quando Z 1=2,4-j 0,7 Ω ;Z 2=8+j 6Ω ;eZ 3=20 +j 0Ω .: