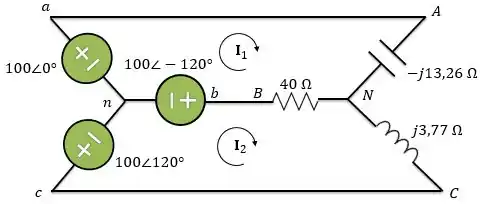
A fonte do circuito abaixo está equilibrada e apresenta uma sequência de fases positiva. Se , determine , e .
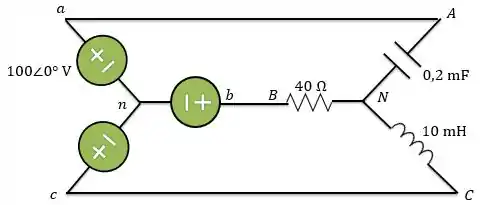
Passo 1
Primeiro, vamos determinar as impedâncias correspondentes ao capacitor e ao indutor.
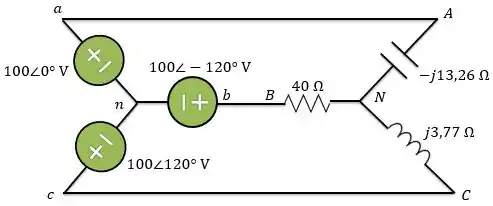
Além disso, como a sequência de fase é positiva, as tensões na fonte são:
Então, temos o seguinte circuito:
Passo 2
Para esse circuito vamos utilizar análise de malhas para determinar as correntes de linha. Para isso, vamos escolher os sentidos para as correntes de malha e :
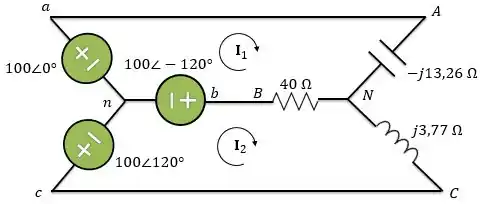
Passo 3
Aplicando a lei das tensões de Kirchhoff na malha , temos:
Passo 4
Aplicando a lei das tensões de Kirchhoff na malha , temos:
Passo 5
Temos duas equações e duas incógnitas. Primeiro, vamos isolar na primeira equação:
Agora, vamos substituir na segunda equação:
Passo 6
Substituindo o valor que encontramos para na equação abaixo, temos:
Passo 7
Aplicando a lei de Ohm podemos encontrar as tensões em cada fase na carga.