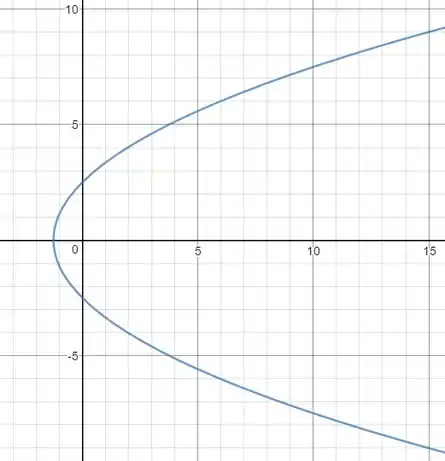
Encontre uma equação em coordenadas polares para a curva cuja equação em coordenadas cartesianas é dada por .
Passo 1
Vamos relembrar as relações entre o sistema cartesiano e o polar:
Belezinha! Agora vamos substituir e na equação do enunciado:
Lembrando que
Uhullll
Resposta