Exercícios Resolvidos de Coordenadas Polares

Exercício 7 1 2 3 4 5 6

Enunciado

Represente graficamente as regiões descritas em coordenadas polares:

e b) e

Passo 1

Esse exercício é um pouco diferente do que vínhamos fazendo!! Agora, não precisamos passar de polares para cartesianas, mas representar a região descrita pelas coordenadas polares.

Passo 2

a) e

Nosso vai de até e nosso ângulo vai de até . Então, se desenharmos teríamos a seguinte figura:

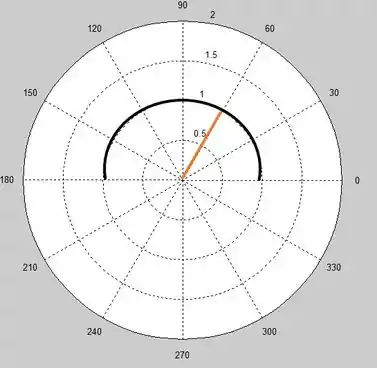
A reta laranja representa o nosso que vai de até . O arco em preto representa a restrição em relação ao nosso ângulo . Então juntado as duas informações sobre e , teremos a seguinte figura:

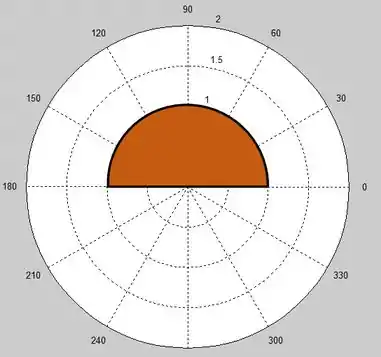
Pronto!! Chegamos na região que as coordenadas polares dadas pelo enunciado representam!!

Passo 3

b) e

Vamos fazer o mesmo procedimento do item anterior. Agora, nosso vai de até , e nosso

ângulo vai de até .

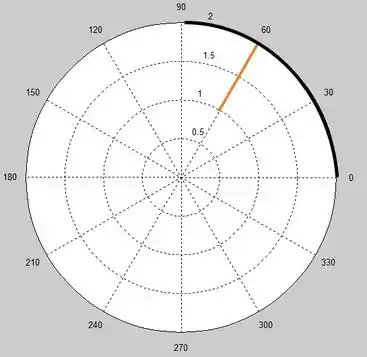
A reta laranja representa o e o arco em preto representa nosso ângulo. Juntando e , temos:

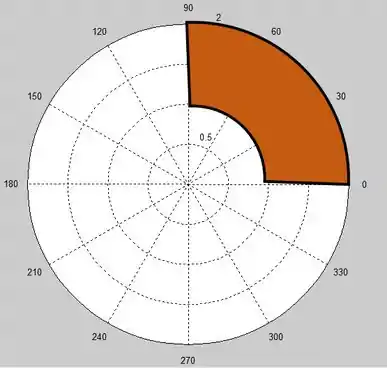
Resposta

Ei, a resposta está no passo a passo :)

Exercícios de Livros Relacionados

Se (x, y) são as coordenadas do ponto P num sistema de eixos ortogonais, quais são as coordenadas polares ( R , θ ) desse ponto?

Identifique o seguinte subconjunto do plano por meio de suas coordenadas polares r , θ : θ = 3 π 4 ,

Descreva o conjunto representado, em coordenadas polares, pela equação R = 3 s i n θ

Num sistema de coordenadas oblíquas em que os semi-eixos positivos formam um ângulo α prove que a rotação do ângulo α em torno da origem leva o segmento O P , onde P = x , y , sobre o segmento O P ' o

Esboce a curva descrita pelo ponto de coordenadas polares R = t eθ = 2 π t quando t assume todos os valores reais positivos.