Identifique a cônica dada em coordenadas polares, determine a sua equação em coordenadas cartesianas e faça um esboço do seu gráfico:
Passo 1
Vamos lá!! O enunciado nos dá uma equação em coordenada polares e a partir dela devemos identificar qual cônica a expressão representa. Além disso, devemos passar a equação para o sistema cartesiano e fazer um esboço do seu gráfico. Bora, começar então?!
Passo 2
Bora lá!

Usando as relações,
Vamos encontrar a equação cartesiana da expressão dada em coordenadas polares:
Da expressão , temos que , que podemos escrever:
Substituindo em , temos:
Reescrevendo, temos:
Como os dois lados da equação estão multiplicados por , podemos cortá-los! Assim,
Elevando os dois lados ao quadrado, temos:
Para chegar na equação final da cônica, vamos completar quadrados!
Dividindo a expressão toda por , temos
Essa é a expressão de uma elipse!! Seu esboço será:
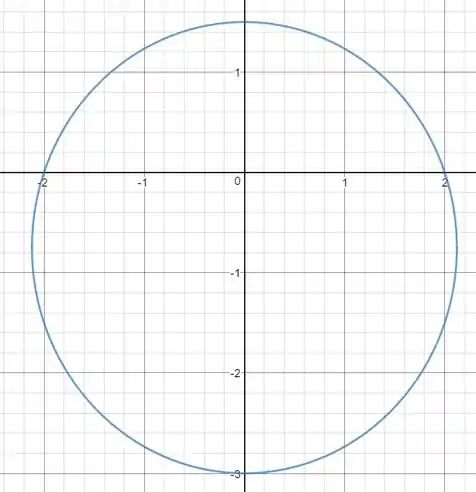
Resposta
Essa é a expressão de uma elipse!!