Identifique a cônica dada em coordenadas polares, determine a sua equação em coordenadas cartesianas e faça um esboço do seu gráfico:
Passo 1
Vamos lá!! O enunciado nos dá três equações em coordenadas polares e a partir delas devemos identificar qual cônica a expressão representa. Além disso, devemos passar a equação para o sistema cartesiano e fazer um esboço do seu gráfico. Bora, começar então?!
Passo 2
Olhando para a expressão fica meio difícil de dizer qual cônica é, certo?!! Então, vamos passar primeiro para o sistema cartesiano já que o jeitão das cônicas nós vimos em coordenadas cartesianas. Para facilitar nossa vida hehe!!

Já que estamos em coordenadas polares e queremos passar para as coordenadas cartesianas, vamos utilizar as seguintes relações que aprendemos na teoria:
Substituindo a expressão na equação dada pelo enunciado, temos:
Pela expressão e rearranjando a mesma, temos:
Substituindo na expressão :
Sabendo da expressão o valor de em função de e , e substituindo na expressão :
Chegamos numa expressão cartesiana agora devemos arrumá-la para que ela fique com o jeitão de alguma das cônicas para que então possamos identificar a cônica:
Completando quadrado temos:
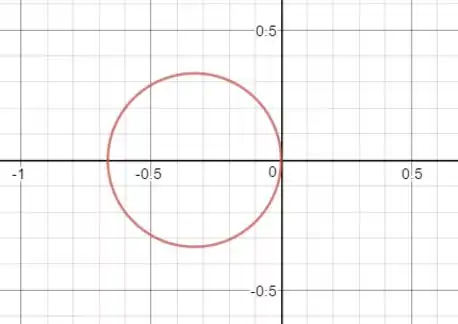
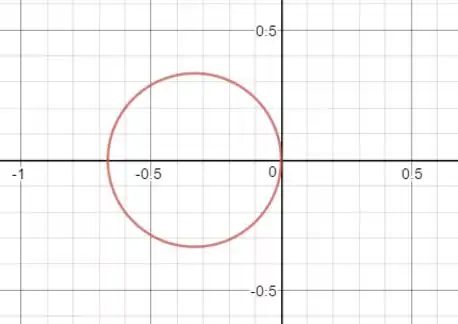
Pela expressão a cônica é um círculo de centro e . Vimos também, que um círculo nada mais é que uma elipse de excentricidade .
Portanto, fazendo um esboço, temos:
Passo 3
O passo a passo é o mesmo do item anterior!! Então, vamos achar primeiro a equação em coordenadas cartesianas!!
Substituindo as relações anteriores e na equação dada pelo enunciado, teremos:
Substituindo , teremos:
Rearranjando a expressão , temos:
Elevando os dois lados ao quadrado:
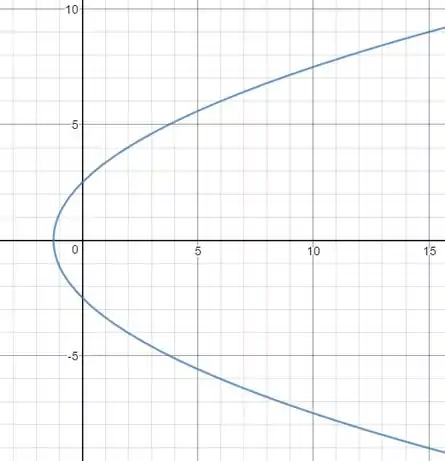
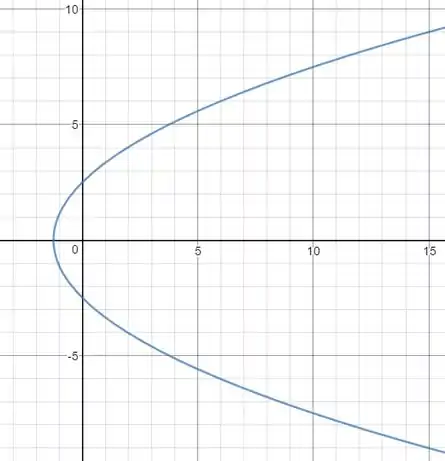
Temos, que representa a origem e , essa segunda expressão representa a parábola:
Então, essa expressão representa uma parábola, fazendo o esboço, temos:
Resposta
- A cônica é um círculo de centro e . Vimos também, que um círculo nada mais é que uma elipse de excentricidade .
- Uma parábola com equação