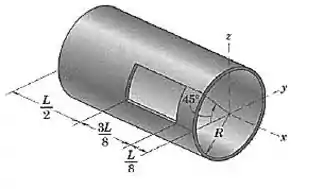
Uma abertura é feita na casca cilíndrica fina. Determine as coordenadas , edo centro de massa do corpo homogêneo.
Passo 1
Vamos começar analisando o pedaço vazio. Qual é a sua área?
Podemos ver na figura que o seu comprimento é de . Mas e a sua largura?
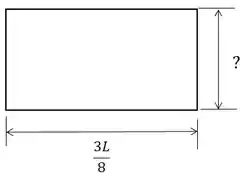
Pela figura podemos ver que alguém pegou o cilindro e girou para cima em torno do eixo . Então, podemos achar a largura do pedaço vazio calculando o comprimento do círculo:
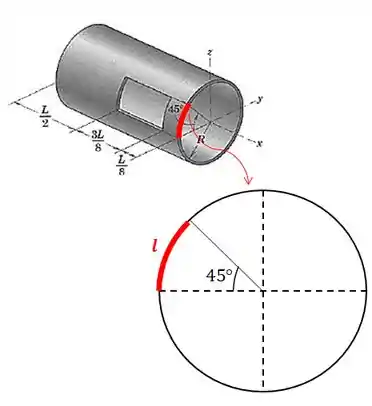
O comprimento de um círculo é calculado por:
No nosso caso, o comprimento do círculo que forma o cilindro é:
Mas isso é para um círculo inteiro, ou seja, com . Mas o comprimento que queremos corresponde a um ângulo de . Então, vamos fazer uma regra de três:
Então:
Beleza?
Então, o pedaço vazi0 com formato de retângulo tem as seguintes medidas:
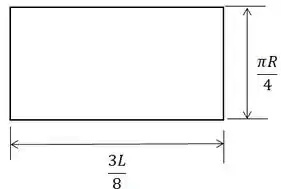
Agora sim podemos calcular a sua área:
Passo 2
Agora temos que achar as coordenadas do centróide do furo retangular. Vamos começar pela coordenada :
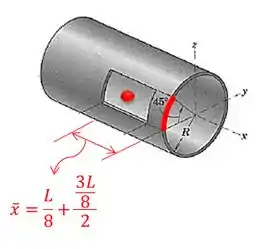
Repare que o centróide do retângulo está na metade do seu comprimento, por isso usamos:
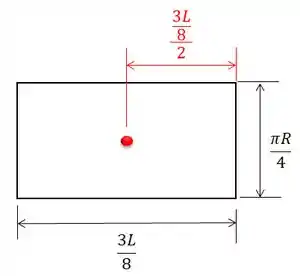
Agora vamos entender o que acontece para acharmos as outras coordenadas do centróide:
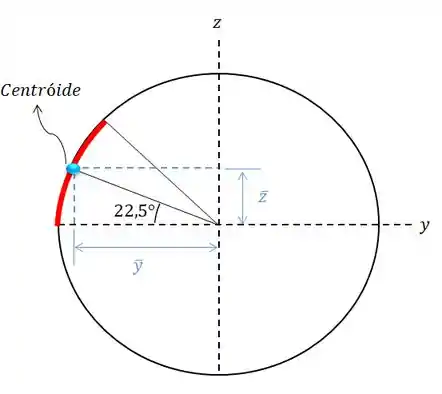
Para calcular e vamos formar um triângulo retângulo, assim:
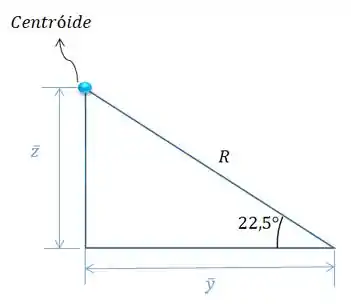
Repare que o ângulo de é a metade de !
Então, vamos ter que é:
Repare que o sinal de menos é porque esta coordenada está posicionada no lado negativo do eixo .
E é:
Passo 3
Agora vamos analisar o cilindro como se não tivesse nenhum furo. A área de um cilindro é calculada assim:
Onde, é o raio e é o comprimento.
Então, a área do nosso cilindro é:
Passo 4
Agora vamos calcular as coordenadas do seu centróide. Sendo que o centróide fica localizado no centro geométrico do cilindro:
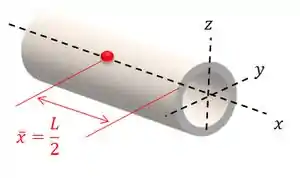
Então, as coordenadas do centróide são:
Passo 5
Agora vamos calcular o centróide do corpo como um todo. Para isso, vamos aplicar as nossas fórmulas pra cada posição:
A coordenada é:
E por último a coordenada :