Determine as coordenadas de centróide da área trapezoidal mostrada.
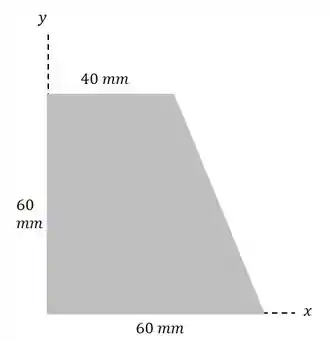
Passo 1
O trapézio pode ser dividido em um retângulo e em um triângulo:
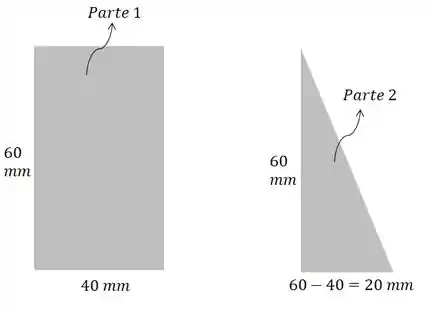
de área:
E um triângulo de área:
Passo 2
Vamos calcular agora a área de cada uma dessas partes. O retângulo tem área igual a:
E o triângulo tem área de:
Como não temos nenhum furo, nenhuma das áreas é negativa.
Vamos preencher a nossa tabela:
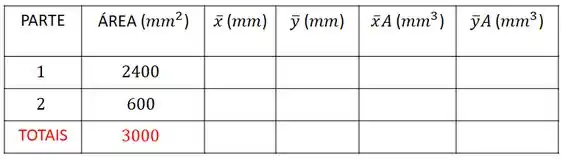
Assim, a área total será a soma das duas áreas:
Passo 3
Agora vamos calcular as coordenadas e do centróide de cada uma das partes que compõe o trapézio.
Vamos começar com o retângulo:
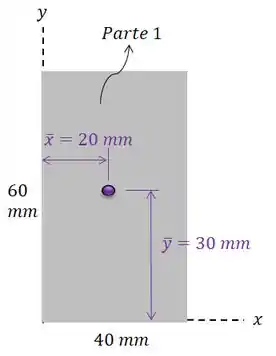
Sabemos que o centróide do retângulo está no seu centro geométrico, ou seja, está na metade da sua altura e está na metade do seu comprimento:
E:
Já o triângulo tem as coordenadas e do centróide à da base e da altura, respectivamente:
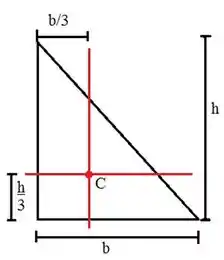
Então, no nosso caso, a coordenada será:
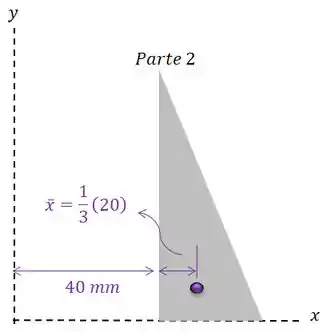
Repare que o eixo está afastado do triângulo e nossa coordenada sempre deve ser com relação ao eixo:
E a coordenada fica:
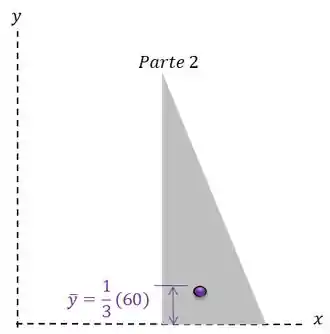
Vamos preencher nossa tabela agora:
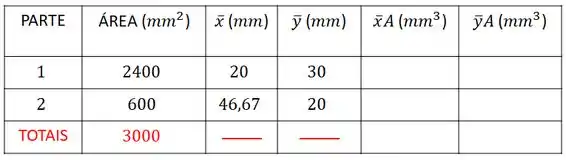
Passo 4
Agora vamos multiplicar cada área por sua respectiva coordenada e . Vamos começar pelo retângulo:
E:
E para o triângulo vamos ter que:
E:
Vamos preencher a nossa tabela com esses valores que achamos:
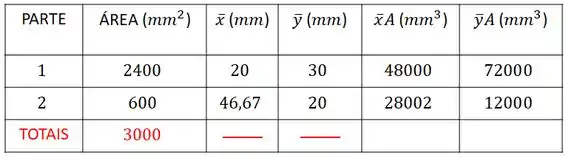
Passo 5
Vamos somar os valores que achamos:
E:
Então, nossa tabela fica:
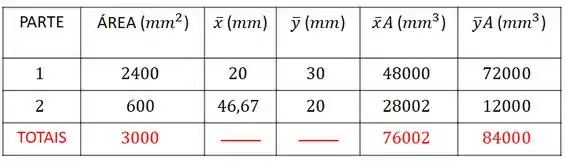
Passo 6
Então, a coordenada será:
E a coordenada do trapézio é: