Um instrumento que trabalha submerso é montado como mostrado na figura. Determine as coordenadas do centróide desse volume composto.
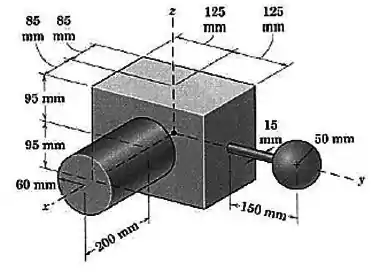
Passo 1
Vamos começar definindo cada parte que compõe este corpo. Vamos começar pelo paralelepípedo:
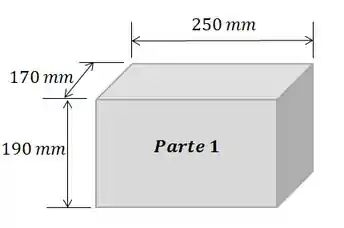
O seu volume será:
Vamos analisar o cilindro maior:
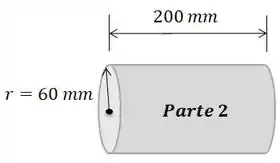
O volume do cilindro é calculado através da seguinte fórmula:
Onde é o seu comprimento.
Então, o volume do nosso cilindro será:
A nossa próxima parte é o cilindro mais fininho:
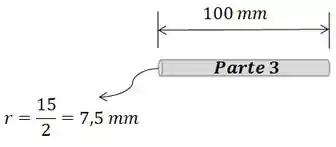
Perceba que para achar o comprimento deste cilindro temos que descontar um pedaço correspondente ao raio da esfera. Então, o seu volume será:
Vamos agora para a nossa quarta e última parte que é a esfera:
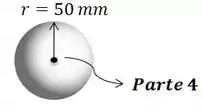
O volume da esfera se calcula assim:
Então, o volume da nossa esfera será:
Passo 2
O próximo passo é calcularmos as coordenadas , e do centróide de cada parte que compõe a figura.
Vamos começar pelo paralelepípedo, sabendo que o seu centróide fica no seu centro geométrico:
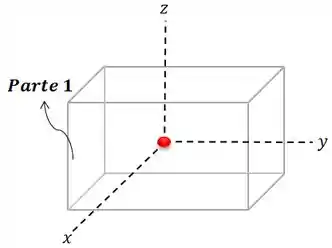
Repare que o centróide está bem na origem dos eixos, então as suas coordenadas são:
Beleza?
Agora vamos ver o cilindro maior:
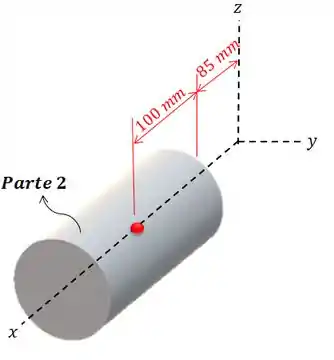
As coordenadas de seu centróide são:
E o cilindro menor fica:
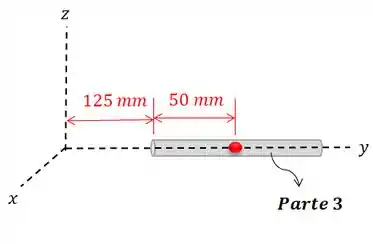
E as coordenadas do centróide deste cilindro são:
E por último temos a esfera:
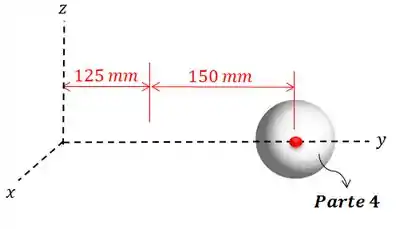
O centróide da esfera também está localizado em seu centro geométrico, então as suas coordenadas são:
Passo 3
Vamos montar a nossa tabela para nos organizarmos:
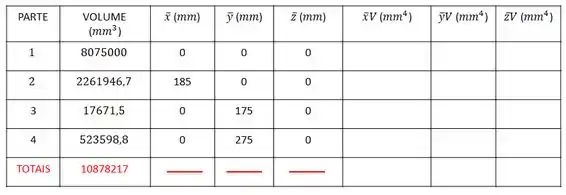
Repare que o volume total é:
Passo 4
Agora temos que multiplicar o volume de cada parte por suas respectivas coordenadas , e do centróide.
- Retângulo:
- Cilindro maior:
- Cilindro menor:
- Esfera:
Passo 5
Nossa tabela ficou assim:
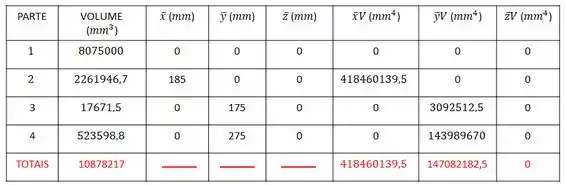
Os totais da tabela são calculados assim:
Temos também:
E por último:
Beleza?
Passo 6
Vamos calcular agora as coordenadas do centróide do sólido como um todo. Para isso, vamos usar as nossas fórmulas.
Vamos começar pela coordenada :
Agora a coordenada :
E por último a coordenada