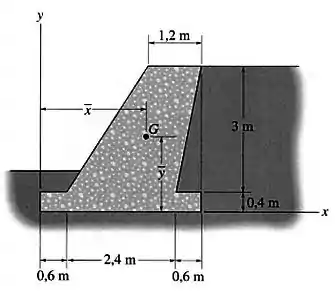
A barragem de gravidade é feita de concreto. Determine a localização do centro de gravidade para a parede.
Passo 1
Vamos começar separando as figuras que compõem a parede e numerá-las:
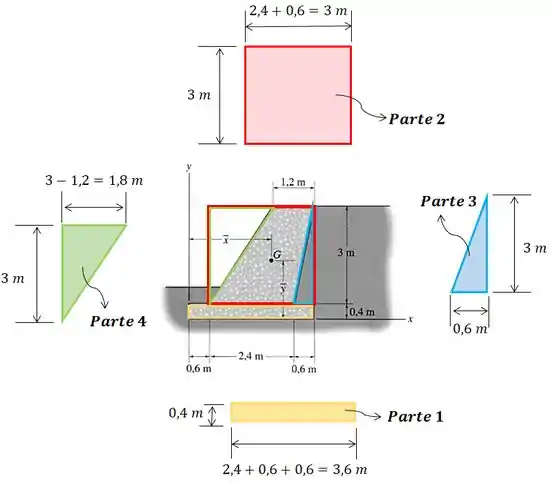
Agora vamos achar a área de cada uma dessas partes:
- Parte 1: é um retângulo, então vamos ter que:
- Parte 2: temos agora um quadrado, então:
- Parte 3: é um triângulo, então:
- Parte 4: temos outro triângulo:
- Parte 1:
- Parte 2:
- Parte 3:
- Parte 4:
- Parte 1:
- Parte 2:
- Parte 3:
- Parte 4:
Não esqueça que a área dos dois triângulos é negativa, pois estas duas figuras não fazem parte da parede, só criamos ela para facilitar nossos cálculos. Então, a nossa tabela fica assim:
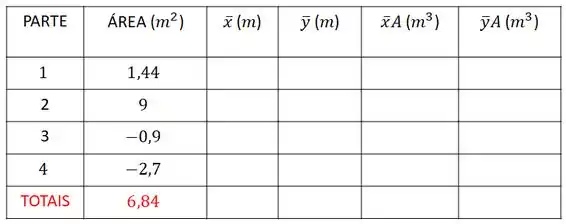
A área total será a soma das quatro áreas:
Passo 2
Agora vamos calcular as coordenadas e do centróide de cada parte que compõe nossa figura. Não se esqueça de que temos que calcular tudo com relação ao eixo que foi dado no enunciado!
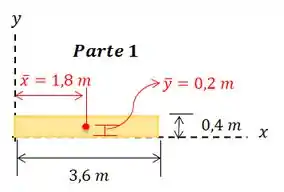
Então:
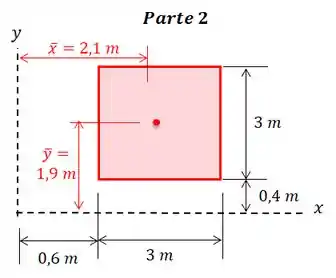
Então:
Para as próximas partes, não podemos esquecer como se calcula as coordenadas do centróide de um triângulo:
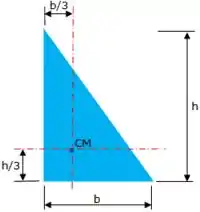
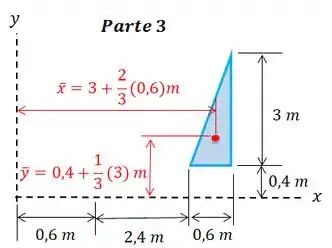
Então:
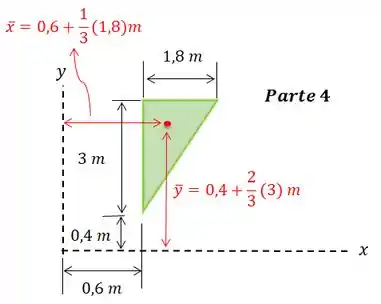
Então:
Vamos colocar isso na nossa tabela:
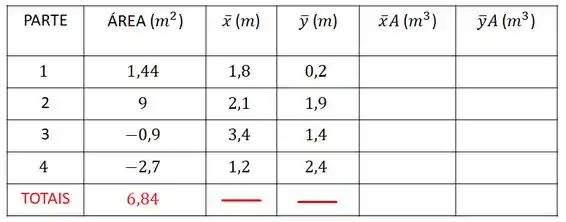
Passo 3
Agora vamos multiplicar cada área por sua respectiva coordenadas e :
Então, a nossa tabela fica assim:
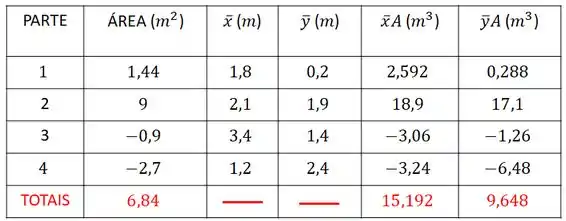
Agora vamos somar os valores que achamos:
E:
Passo 2
Agora é só aplicar a fórmula para acharmos as coordenadas e do centróide da nossa figura.
Então, para vamos ter que:
E para vamos ter que: