Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Corpos Compostos

Ver Teoria
Exercício 61234578

Enunciado

Determine a coordenada y do centróide da área sombreada em função de h .

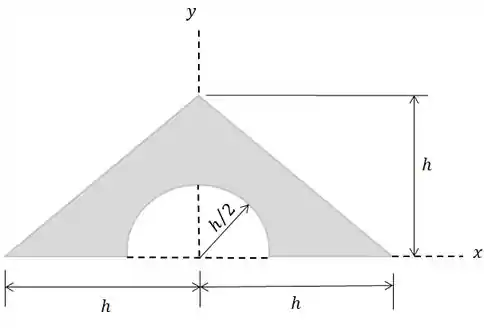
Passo 1

A nossa figura tem duas partes: um triângulo e um furo no formato de um semicírculo. Então, vamos começar pelo triângulo:

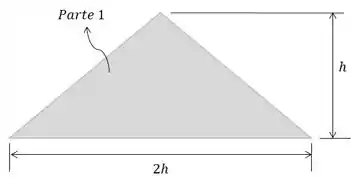
A área do triângulo é dada por:

A 1 = ( 2 h ) ( h ) 2 = h 2

Nossa segunda parte é um semicírculo:

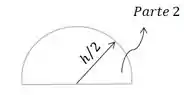
E sua área é dada por:

A 2 = π r 2 2       →           A 2 = π 2 h 2 2

∴

A 2 = π h 2 8

Não esqueça que a área do semicírculo é negativa, pois ele é um furo. Então, a nossa tabela fica assim:

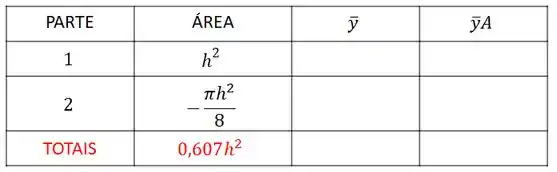
A área total será a soma das duas áreas:

∑ A = h 2 - π h 2 8       →         ∑ A = 0,603 h 2

Passo 2

Agora vamos calcular a coordenada y - do centróide de cada parte que compõe nossa figura. Vamos começar com o triângulo, mas para isso você tem que lembrar que a coordenada y - do centróide de um triângulo fica a 1 3 da altura:

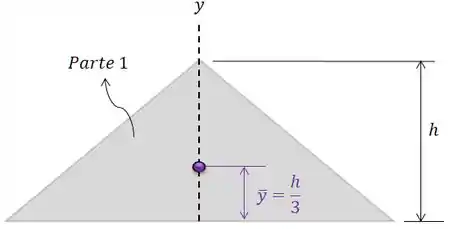
Então:

y - = h 3

E o centróide do semicírculo é calculado pela seguinte fórmula:

y - = 4 r 3 π       →         y - = 4 h 2 3 π

∴

y - = 2 h 3 π

Vamos colocar isso na nossa tabela:

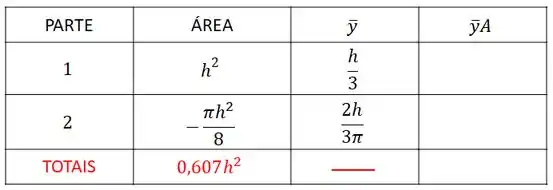
Passo 3

Agora vamos multiplicar cada área por sua respectiva coordenada x - e y - . Vamos começar pelo triângulo:

A 1 y - = h 2 h 3         →           A 1 y - = h 3 3

E o semicírculo fica assim:

A 2 y - = - π h 2 8 2 h 3 π     →           A 2 y - = - h 3 12

Então, a nossa tabela fica:

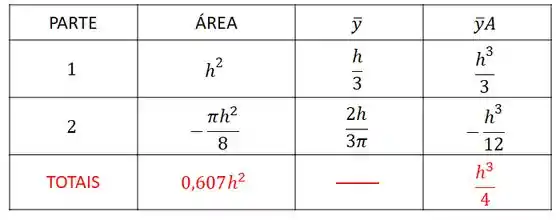
Vamos somar os valores que achamos:

∑ y - A = h 3 3 - h 3 12           →           ∑ y - A = h 3 4  

Passo 4

Agora é só aplicar a fórmula para acharmos a coordenada Y - do centróide da nossa figura:

Y - = ∑ y - A ∑ A         →       Y - = h 3 4 0,607 h 2

∴

Y - = 0,412 h

Resposta

Y - = 0,412 h

Exercícios de Livros Relacionados

Um pedreiro estica uma corda entre dois pontos separados por 50 pés no mesmo nível com uma tensão de 10 libras em cada extremidade. Se a corda pesa 0,1 lb, determine a flexão h no meio da corda.
Determine a localização y do eixo x–x que passa pelo centroide da área transversal da viga. Para o cálculo, desconsidere o tamanho das soldas nos cantos em A e B.
Encontre o centroide do fio.
Cada um dos três membros da estrutura tem uma massa por unidade de comprimento de 6 k g / m . Localize a posição do centro de massa. Despreze a dimensão dos pinos nas juntas e a espessura dos membros.
Desenhe os diagramas de cortante e momento para a viga carregada e encontre a magnitude máxima M do momento fletor.