Calcule a coordenada do centróide da área sombreada.
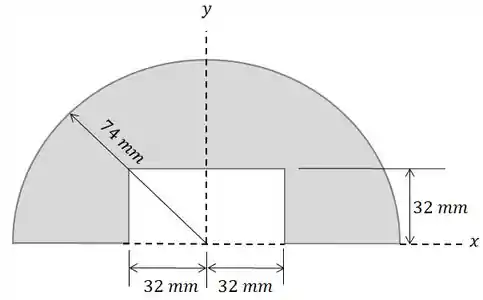
Passo 1
Nessa figura temos duas partes: um semicírculo e um furo de formato retangular. Então, vamos nomear as partes:
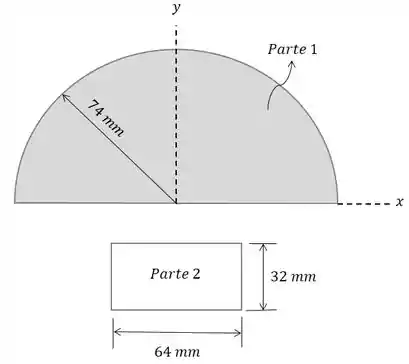
Passo 2
Agora temos que calcular a área de cada parte que compõe nossa figura. A parte é um semicírculo, então:
E a área da parte será:
Mas não se esqueça que como a área retangular é um furo, ela terá uma área negativa.
Nossa tabela fica assim, então:
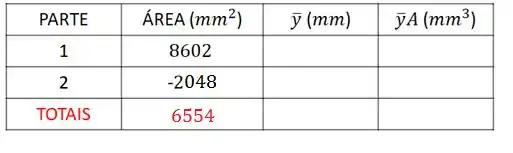
Para achar o total é só subtrair a área do furo da área do semicírculo:
Passo 3
Perceba que a figura é simétrica em relação ao eixo , ou seja, a coordenada
Então só precisamos achar (e também foi o que a questão pediu!)

Aqui você precisa saber que o centróide de um semicírculo é dado pela seguinte fórmula (que você pode encontrar em qualquer tabela de centróide):
Então, substituindo , temos que:
E a coordenada de um retângulo nós sabemos que fica na metade de sua altura, então:
Vamos colocar esses valores na nossa tabela:
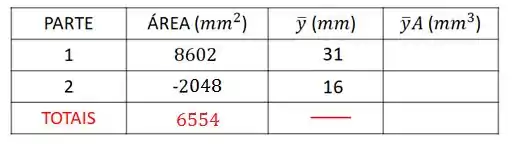
Passo 4
Agora temos que multiplicar cada coordenada pela sua respectiva área:
E:
Colocando isso na tabela, temos:
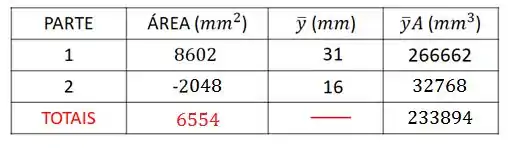
E o total é só somarmos os dois resultados, lembrando que é negativo!
Então:
Passo 5
Agora é só calcularmos a coordenada da nossa figura: