A correlação , desenvolvida para calcular o coeficiente de transferência de calor por convecção, , entre uma partícula esférica e um fluido em escoamento, pode também ser utilizada, por analogia, para o cálculo do coeficiente de transferência de massa, . Sabe-se que o Número de Sherwood, , é equivalente ao Número de Nusselt, ; o Número de Schmidt, , é equivalente ao Número de Prandtl, ; é o Número de Reynolds. Considerando o exposto, analise cada uma das afirmações a seguir, julgando-as como verdadeiras ou falsas e justificando sua resposta:
I - Para valores muito baixos de , pode ser obtido por , onde é o coeficiente de difusão molecular de A em uma mistura de A e B, e é o diâmetro da partícula esférica.
II - Para valores muito altos de , pode ser obtido por , onde é o coeficiente de difusão molecular de A em uma mistura de A e B, é o diâmetro da partícula esférica, é a viscosidade cinemática do fluido em escoamento e a velocidade no seio do fluido.
III - , que representa a razão entre as difusividades inercial (momentum) e molecular (de massa), pode ter unidades de .
IV – As melhores estimativas teóricas para provêm da teoria da camada limite.
V – A analogia de Chilton-Colburn pode ser encarada com uma extensão da analogia de Reynolds para , sendo considerada a mais adequada para a previsão de em fenômenos descritos pela teoria da camada limite.
Passo 1
Fala aí!! Partiu encarar esse desafio juntos! Precisamos verificar cada uma dessas opções e dizer se elas são verdadeiras ou falsas, ok?
Vamos começar com a primeira, ela diz que se tivermos valores muito baixos de Reynolds, então o pode calculado por essa fórmula aqui: … Bom, pra começo de conversa vamos reescrever a equação de transferência de calor dada no enunciado, na forma de equação de transferência de massa, baseado nas informações que o problema nos deu, ok?
Vamos lembrar lá da nossa teoria, que essa equação só pode ser aplicada se essas condições forem respeitadas: e , belezinha?
Bom, mas essa opção tá falando do coeficiente convectivo… relembrando que podemos usar a relação, para placa plana, onde:
Arrumando e substituindo o comprimento da placa pelo diâmetro da partícula esférica, vamos ficar com:
Então essa opção está dizendo que para valores de Reynolds muito baixos, vamos ter que:
E sendo assim, acabamos de verificar que essa opção está correta!
Passo 2
Agora vamos para a segunda opção! Ela diz que para valores muito altos de , pode ser obtido por , vamos verificar, sendo:
E substituindo a equação de Sherwood , vamos ter:
Substituindo o número de Reynolds, como sendo:
Vamos ter:
E substituindo também o número de Schmidt:
Ficamos com:
Arrumando essa bagunça toda, ficamos com:
Então nossa segunda alternativa também está correta!
Passo 3
Essa terceira está mais para uma pegadinha, né? Olha só, ela tá dizendo que o número de Schmidt, , pode ter unidades de … Maaaasss a gente sabe que o número de Schmidt é adimensional! Logo ele não tem unidades! E essa opção é falsa!
Passo 4
Agora a nossa quarta opção. Ela diz que as melhores estimativas teóricas para provêm da teoria da camada limite… E essa é uma afirmação que vemos na prática que é verdade! Pois a teoria da camada limite, respeitando as formas de cada escoamento, é uma ótima maneira de encontrar o se a gente não tiver trabalhando com dados experimentais!
Passo 5
Pra fechar, vamos para a última opção! Ela nos afirma que a analogia de Chilton-Colburn pode ser uma extensão da analogia de Reynolds para , sendo considerada a mais adequada para a previsão de em fenômenos descritos pela teoria da camada limite.
Bom, a primeira parte dela a gente sabe de cara que está correta, porque aprendemos isso em teorias anteriores, né? Beleza! Sabemos que sim a analogia de Chilton-Colburn é uma extensão da analogia de Reynolds, mas considerando . Mas agora ela diz que ela representa melhor a teoria da camada limite… hummm… Vamos observar essa imagem aqui:
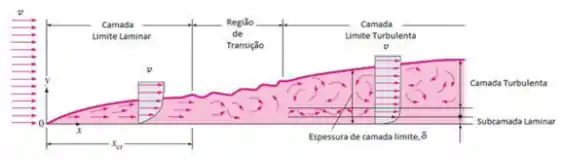
Ela mostra representa a teoria da camada limite e mostra pra gente que temos uma camada laminar, uma região de transição e uma camada turbulenta, bom a analogia de Reynolds não considera, justamente, essa região de transição, enquanto que a analogia de Chilton-Colburn considera. Então, essa afirmação é verdadeira sim!
Resposta
- Verdadeiro
- Verdadeiro
- Falso
- Verdadeiro
- Verdadeiro