Dado o elemento abaixo, determine o fator de segurança pelo método de Tresca e de Von Mises sabendo que a resistência desse material é de
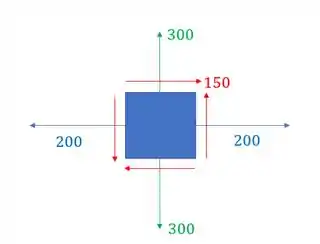
Passo 1
Sabemos que tanto o critério de Tresca, quanto o critério de Von mises dependem das tensões principais que agem nesse elemento, sendo em um necessário a tensão cisalhante máxima, e no outro, sendo necessário a tensão principal maior e menor. Relembrando as fórmulas teremos que
Para o critério de Tresca
Em que sabemos que
E para o critério de Von Mises
Em que também sabemos que
Sabemos pelo enunciado que
Passo 2
Agora temos que determinar as tensões principais para podermos fazer o cálculo dos fatores de segurança
Sabemos que
Então
Também sabemos que
Logo
Passo 3
Como já temos esses valores, podemos facilmente determinar os valores das tensões máximas pelas fórmulas
Substituindo
O cisalhante máximo é muito simples, é o próprio valor do R que já calculamos
Passo 4
Agora que já temos todos os valores já podemos fazer as devidas substituições
Primeiro vamos calcular o fator de segurança pelo critério de Tresca.
Substituindo na nossa fórmula teremos que
Passo 5
Pelo critério de Von Mises teremos que o fator de segurança será
Sabemos que
E
Então nosso fator de segurança será
Resposta
Fator de segurança por Tresca
Fator de segurança por Von Mises