Determine o fator de segurança para o elemento abaixo, sabendo que . Use o critério de tresca e de Von mises para isso.
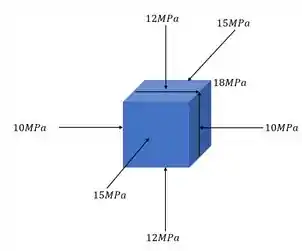
Passo 1
Sabemos que tanto o critério de Tresca, quanto o critério de Von mises dependem das tensões principais que agem nesse elemento, sendo em um necessário a tensão cisalhante máxima, e no outro, sendo necessário a tensão principal maior e menor. Relembrando as fórmulas teremos que
Para o critério de Tresca
Em que sabemos que
E para o critério de Von Mises
Em que também sabemos que
Sabemos pelo enunciado que
Passo 2
Sabemos que como apresenta-se tensão cisalhante em alguns planos, estes não poderão ser considerados planos principais.
O que podemos afirmar é que o plano sem tensões cisalhantes é de fato um plano principal, podemos então afirmar que
Mas como determinar as tensões principais referentes aos outros planos?
Passo 3
Basta usarmos os conceitos aprendidos na aula de transformação de tensões.
Basta analisar o seguinte elemento infinitesimal dado pelos esforços que agem nos planos com cisalhante.
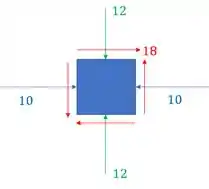
Agora é só determinar as tensões principais presentes nesse elemento infinitesimal.
Passo 4
Sabemos que para determinarmos as tensões principais precisamos usar
Que nos fornece a média das tensões
Que nós dá o cisalhante máximo que o nosso elemento foi submetido
A última fórmula é dada por
Que de fato nos fornece o valor das tensões principais
Sabemos que
Substituindo teremos que
Organizando teremos que
Mas também precisamos do valor de tensões cisalhantes máxima
Passo 5
Agora vamos determinar o fator de segurança pelo critério de Tresca
Sabemos que
Substituindo na nossa fórmula teremos que
Passo 6
Pelo critério de Von Mises teremos que o fator de segurança será
Sabemos que
E
Então nosso fator de segurança será
Resposta
Fator de segurança por Tresca
Fator de segurança por Von Mises