No estado plano de tensões de um ponto , as tensões principais são e .
Determine, usando os critérios de Tresca e de von Mises, o coeficiente de segurança para esse ponto sabendo que ele é feito de um material que possui um limite de resistência ao escoamento .
Ao final, esboce o hexágono de Tresca e a elipse de von Mises para esse material e mostre a localização do ponto nesses gráficos.
Passo 1
O que está acontecendo?
O exercício nos forneceu as tensões principais em um ponto :
Sendo que, lembra aí, a partir dessas tensões principais máximas e mínimas em um ponto, é possível determinar a tensão cisalhante máxima nesse ponto:
Onde e são as tensões principais máxima e mínima nesse ponto.
Além disso, o exercício ainda nos fornece o limite de resistência ao escoamento desse material.
Sendo que, lembra aí, a partir desse limite , é possível encontrar o limite de resistência ao escoamento por cisalhamento, :
E o que é que o exercício quer?
Ele quer que a gente determine os coeficientes/fatores de segurança para esse ponto usando os critérios de Tresca e de von Mises.
Para tanto, devemos usar as fórmulas:
Lembrando que é o que chamamos de tensão de von Mises, que é definida para um estado plano de tensões como:
Ao final, o exercício ainda quer que a gente esboce o hexágono de Tresca e a elipse de von Mises:
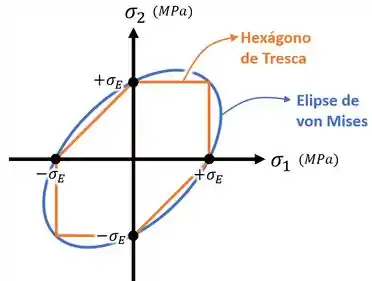
...e mostre a localização do ponto nesse gráfico.
Passo 2
Então vamos lá!
Primeiro, para calcular o fator de segurança de acordo com o critério de Tresca, precisamos calcular:
- O limite de resistência ao escoamento por cisalhamento, :
- E a tensão de cisalhamento máxima no ponto:
Para esse ponto, nós vamos ter as tensões principais no plano , e uma tensão principal no eixo fora do plano de .
Sendo assim, a tensão principal máxima no ponto vai ser e a mínima , de tal forma que:
Feito isso, podemos agora fazer que:
O que vai dar:
O que significa que, pelo critério de Tresca, o material possui vezes a resistência que ele necessita ter.
Passo 3
Agora, para calcular o fator de segurança de acordo com o critério de von Mises, precisamos calcular a tensão de von Mises:
Substituindo e , isso fica assim:
Simplificando os sinais, temos:
E calculando tudo, encontramos que:
Feito isso, podemos agora aplicar:
Substituindo e , encontramos que:
O que dá:
O que significa que, pelo critério de von Mises, o material possui vezes a resistência que ele precisa ter.
Passo 4
Por fim, para completar o exercício, só falta desenharmos o hexágono de Tresca e a elipse de von Mises, usando para tanto que :
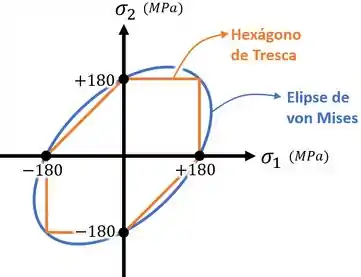
Aí, marcando as tensões principais e do ponto nesse gráfico, confirmamos como o ponto não falha de acordo com nenhum critério:
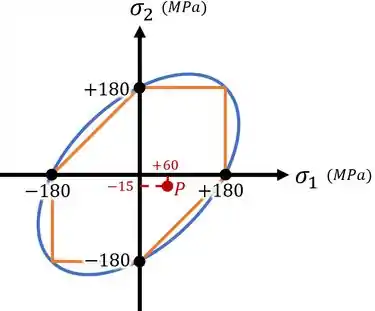
E assim terminamos nosso exercício!