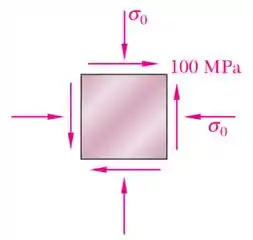
O estado plano de tensão indicado ocorre em um componente de máquina feito de um aço com . Usando os critérios da tensão de cisalhamento máxima (critério de Tresca) e da energia de distorção máxima (critério de Von-Mises), determine se ocorre o escoamento quando:
;
& .
Caso o escoamento não ocorra, determine o coeficiente de segurança correspondente.
Passo 1
O que está acontecendo?
O exercício nos forneceu um estado plano de tensões para um ponto em que:
Sendo que esse ponto é feito de um aço com um limite de resistência ao escoamento .
E o que é que o exercício quer?
Ele quer que a gente determine os coeficientes/fatores de segurança desse ponto acordo com os critérios de Tresca e de von Mises para as situações em que:
;
& .
Sendo que, caso um desses fatores de segurança seja menor do que 1, isso vai significar que vai ter ocorrido o escoamento do material.
Então, para resolver o exercício...
Devemos primeiro calcular as tensões principais nesse ponto em função de .
Feito isso, vamos poder calcular os fatores de segurança para cada valor de de acordo com os critérios de Tresca e de von Mises usando as fórmulas:
Sendo que é importante lembrar que:
E que, para um estado plano de tensões:
Passo 2
Então vamos lá!
Antes de tudo, precisamos determinar as tensões principais no nosso ponto em função de , então vamos fazer isso.
Lembra aí!
Para determinar as tensões principais no estado plano de tensões, podemos:
1. Calcular a tensão normal média no ponto:
Aí aqui, substituindo que , vamos encontrar que:
& 2. Calcular o raio para esse estado de tensões:
Aí, aqui, como , isso vai ficar assim:
O que significa que:
E como , isso significa que:
Feito isso, podemos agora calcular as nossas tensões principais aplicando que:
Aí, substituindo e , vamos encontrar que:
Passo 3
Definidas as tensões principais, podemos agora resolver o item .
Nesse item, temos que , de tal forma que:
Agora, além dessas duas tensões principais no plano, ainda vai haver no ponto uma terceira tensão principal no eixo fora do plano de .
Dessa forma, as tensões principais máxima e mínima para esse ponto são:
Passo 4
Em seguida, para calcularmos o coeficiente/fator de segurança de Tresca, precisamos calcular os termos:
O que, substituindo vai dar:
Aí, usando esses valores para calcular o coeficiente/fator de segurança de Tresca, encontramos que:
O que dá:
Passo 5
Para finalizar o item , devemos calcular o coeficiente/fator de segurança de von Mises.
Para tanto, devemos antes calcular a tensão de von Mises :
Substituindo e e simplificando os sinais, obtemos que:
O que vai dar:
Aí, usando esse valor e para calcular o coeficiente/fator de segurança de von Mises, temos:
O que dá:
Passo 6
Terminado o item , podemos seguir para o item .
Nesse item, temos que , de tal forma que:
Agora (mais uma vez!), além dessas duas tensões principais acima no plano, ainda vai haver no ponto uma terceira tensão principal no eixo fora do plano de .
Dessa forma, as tensões principais máxima e mínima para o ponto são:
Passo 7
Agora, com o objetivo de calcular o coeficiente de segurança de Tresca, precisamos calcular antes a tensão de cisalhamento máxima nesse ponto do item :
Aí, usando esse valor e o valor já calculado lá no passo 4, podemos calcular o coeficiente de segurança de Tresca:
Obtendo assim que:
Sendo que, como esse valor está abaixo de , ele significa que o material do ponto vai escoar/falhar pelo critério de Tresca.
Passo 8
E finalmente, para terminar o exercício, vamos calcular o coeficiente de segurança de von Mises para o item , começando pelo cálculo da tensão de von Mises para esse item:
Substituindo e e simplificando os sinais, obtemos que:
O que dá:
Aí, usando esse valor e para calcular o coeficiente/fator de segurança de von Mises, temos:
E pronto!
Terminamos o exercício.
Resposta
Pelos critérios de Tresca e Von-Mises, temos coeficientes de segurança e , respectivamente.
Pelo critério de Tresca, ocorre o escoamento do material. Já pelo critério de Von-Mises, temos um coeficiente de segurança .