Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Curvas Abertas

Ver Teoria
Exercício 712345689101112131415

Enunciado

Calcule a integral de linha vetorial ∮ γ F → d r → , onde

F → x , y , z = e x 2 - 3 y z + x ,   e y 2 + x z + y ,   - e z 2 - x y + z

E γ é a intersecção, no primeiro octante, do cilindro x 2 + y 2 = 2 x e com o plano x = z , do ponto inicial 0 ,   0 ,   0 até o ponto final ( 2 ,   0 ,   2 ) . (Obs.: cos 2 ⁡ θ = 1 2 ( 1 + cos ⁡ 2 θ ) e cos 4 ⁡ θ = 1 8 ( cos ⁡ 4 θ + 4 cos ⁡ 2 θ + 3 ) . )

Passo 1

Para a gente ter uma noção clara do que vamos ter que fazer, é legal a gente ter uma boa visão de γ , certo? Então me acompanha aqui!

Bem... γ   é a intersecção do cilindro x 2 + y 2 = 2 x com o plano x = z . E esse cilindro está deslocado uma unidade em x , se lembra?

x 2 + y 2 = 2 x   ⇒       x 2 - 2 x + y 2 = 0     ⇒

Completando quadrado...

x - 1 2 - 1 + y 2 = 0     ⇒         x - 1 2 + y 2 = 1    

Fazendo a intersecção com o plano x = z que é um plano paralelo ao eixo y , e lembrando que queremos apenas o primeiro octante, obteremos a γ em amarelo. :D

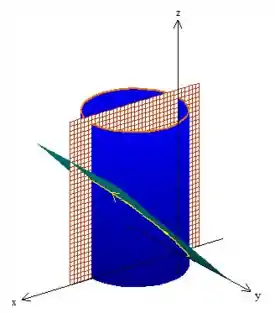
Passo 2

Podemos ver que resolver aquele integral de linha direto pode nos dar muita dor da cabeça! Logo a gente vai recorrer a um método alternativo: ao teorema de Stokes que nos diz o seguinte

∮ ∂ S F → d r → = ∯ S r o t   F → ∙ n → d S

Onde

  • ∂ S é a borda de uma superfície fechada S
  • n → são os vetores normais a S orientada positivamente
  • r o t   F → é o rotacional do campo não singular (o campo que temos é não singular!:D)

Passo 3

Começando pelo ∂ S , devemos escolher uma superfície fechada que tenha como borda, justamente a curva γ que queremos simplificar.

Ora! A superfície mais simples que faz isso é justamente a que está em cima do plano que delimita γ

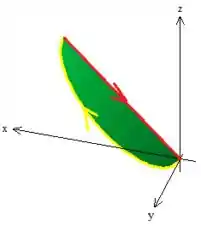
Cuidado! Essa orientação de toda borda deve ser a mesma pedida no exercício, okay?

∂ S = γ ∪ γ 1

Logo, do primeiro lado da equação de Stokes acima, teremos ∮ ∂ S F → d r → = ∮ γ F → d r → + ∮ γ 1 F → d r → :

∮ γ F → d r → + ∮ γ 1 F → d r → = ∯ S r o t   F → ∙ n → d S

Portanto, pra gente encontrar o resultado que a gente quer, vamos calcular essas outras duais integrais aí e ver no que dá! :)

Passo 4

Vamos começar com a integral de superfície, e, portanto, a parametrizando.

Como a superfície S está delimitada pelo cilindro, podemos pensar em uma parametrização em coordenadas cilíndricas (Mas lembre-se!: o cilindro está deslocado)

x - 1 = r cos ⁡ θ  

y = r sin ⁡ θ

Como na superfície S , z = x

z = 1 + r cos ⁡ θ

Logo,

φ r ,   θ = ( 1 + r cos ⁡ θ ,   r sin ⁡ θ ,   1 + r cos ⁡ θ )

Onde r varia até chegar o raio máximo do cilindro e θ dá uma meia volta, ou seja,

0 ≤ r ≤ 1

0 ≤ θ ≤ π

Passo 5

Vamos prosseguir calculando o r o t   F → .

Lembrando da fórmula da rotacional de um campo e calculando as integrais a gente vai ter

r o t   F → = ∂ F 3 → ∂ y - ∂ F 2 → ∂ z ,   ∂ F 1 → ∂ z - ∂ F 3 → ∂ x ,   ∂ F 2 → ∂ x - ∂ F 1 → ∂ y

r o t   F → = - x - x ,   - 3 y - - y ,   z - ( - 3 z )

r o t   F → = - 2 x , - 2 y , 4 z

Ótimo! O rotacional realmente simplifica a nossa vida. Vamos ver se o vetor normal faz o mesmo?

n → = ∂ φ ∂ r × ∂ φ ∂ θ

Calculando essas derivadas parciais da superfície

∂ φ ∂ r r ,   θ = ( cos ⁡ θ , sin ⁡ θ , cos ⁡ θ )

∂ φ ∂ θ r ,   θ = ( - r sin ⁡ θ ,   r cos ⁡ θ ,   - r sin ⁡ θ )

E jogando no determinante esses vetores e;

n → = i ^ j ^ k ^ cos ⁡ θ sin ⁡ θ cos ⁡ θ - r sin ⁡ θ r cos ⁡ θ - r sin ⁡ θ =

Calculando... vamos obter

n → = - r ,   0 ,   r

Observe que precisamos de mudar o sinal do vetor normal porque a curva está orientanda negativamente, logo, pela regrada mão direita precisamos da coordenada z negativa, ou seja

n → = r ,   0 ,   - r

Passo 6

Jogando tudo na integral de superfície e resolvendo o produto interno do rotacional com vetor normal:

∯ S r o t   F → ∙ n → d S = ∫ 0 π ∫ 0 1 - 2 x , - 2 y , 4 z ∙ r ,   0 ,   - r d r d θ

Note que a única coordenada que nos interessa é a primeira e a última, pois elas não vão zerar, porém... precisamos mudar as coordenadas z e y para as coordenadas polares

∫ 0 π ∫ 0 1 - 2 r 1 + r cos ⁡ θ - 4 r 1 + r cos ⁡ θ d r d θ = - 6 ∫ 0 π ∫ 0 1 r + r 2 cos ⁡ θ d r d θ

Em θ a gente mata a integral mole e em r é um polinômio, logo a gente mata fácil

- 6 ∫ 0 π r 2 2 + r 3 3 cos ⁡ θ 0 1 d θ = - 6 ∫ 0 π 1 2 + cos ⁡ θ 3 d θ =

= - 6 θ 2 + sen ⁡ θ 3 0 π = - 6 π 2 + 0 - 0 - 0 = - 3 π

∯ S r o t   F → ∙ n → d S = - 3 π

Passo 7

Agora falta pra gente a integral de linha ∮ γ 1 F → d r → , que eu prometo ser mais simples!;)

Vamos começar parametrizando essa curva γ 1 que é uma reta onde y = 0 e x = z , pois ela está em cima do plano

Logo

σ t = ( t ,   0 ,   t )

Onde x = t então t vai de 2 até 0 , pois queremos que a reta vá do ponto 2,0 , 2 até o 0,0 , 0 !

Agora derivando a superfície para obter o termo d r → = σ ' t d t

σ ' t = ( 1 ,   0 ,   1 )

Bem... não esquecendo de aplicar no campo vetorial F → a parametrização, podemos, por fim, ir para a integral

∮ γ 1 F → d r → = ∮ γ 1 F → ( σ t ) σ ' t d t = ∫ 2 0 e t 2 + t ,   1 + t 2 ,   - e t 2 + t ∙ 1 ,   0 ,   1 d t

Resolvendo esse produto interno...

∮ γ 1 F → d r → = ∫ 2 0 e t 2 + t - e t 2 + t d t

∮ γ 1 F → d r → = ∫ 2 0 2 t   d t

∮ γ 1 F → d r → = t 2 2 0 = - 4

Conforme prometido, está aí! ;)

Passo 8

Agora voltando para o nosso problema e substituindo tudo nas integrais...

∮ γ F → d r → + ∮ γ 1 F → d r → = ∯ S r o t   F → ∙ n → d S

∮ γ F → d r → - 4 = - 3 π

∮ γ F → d r → = 4 - 3 π

Resposta

∮ γ F → d r → = 4 - 3 π