Calcule onde e é parametrizada por ,
Passo 1
Vamos lá galera, essa curva ai dá pra perceber que é aberta, não é? O esboço dela pode ser meio complicado, mas só de substituir e vemos que o começo e o fim são diferentes
O esboço é esse aqui

Parece meio bizarro tentar fazer essa integral de linha diretamente, né? Vamos ver como é o rotacional de pra ver se vale a pena usar o teorema de Stokes
Perfeito! Com esse rotacional nulo o teorema de Stokes parece ser o método mais simples, não é? Precisamos então fechar essa curva.
Geralmente fechamos a curva com uma reta que ligue as duas extremidades. Nessa questão aqui, a reta que liga esses dois pontos é um pouco complexa. Vamos ver que fechar com duas retas mais simples fica mais fácil, olha só
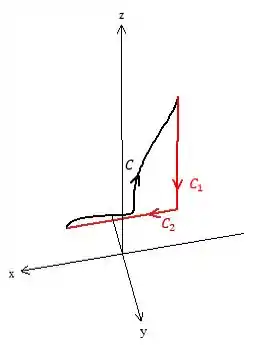
Isso pode ser feito porque o rotacional é nulo! Então não precisamos nos preocupar com a integral da superfície gerada. Só pra deixar claro, varia só no eixo e varia só no eixo
O teorema de Stokes fica assim
Passo 2
Vamos começar então com a reta , vamos precisar de uma parametrização para calcular essa integral. Depois é só calcular o campo em função dos parâmetros e jogar na integral.
A reta vai do ponto até o ponto , certo? O vetor direção é essa aqui
Podemos parametrizar essa reta como
O campo com os novos parâmetros fica
Agora é só jogar esse valor na integral, junto da derivada da parametrização
Passo 3
Vamos para a próxima curva, seguindo o mesmo passo a passo. Precisamos primeiramente da parametrização da reta que vai do ponto até o ponto . O vetor direção é esse aqui
A parametrização fica
O campo com os novos parâmetros fica
A integral vai ficar isso aqui
Passo 4
Beleza, agora é só voltar pro teorema de Stokes