Use o teorema de Stokes para Calcular o trabalho do campo
ao longo da curva parametrizada por com .
Passo 1
Já que o enunciado mandou a gente resolver pelo teorema de Stokes, vamos começar logo pelo rotacional, já que isso é uma certeza que a gente vai calcular mais cedo ou mais tarde.
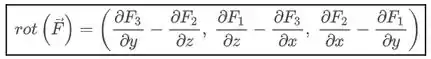
Opa, maneiro que é um rotacional tranquilo de trabalhar.
Passo 2
Bom, pelo teorema temos as condições a cumprir.
- Curva fechada
- Orientação positiva
- Campo sem singularidade.
Quanto a orientação, vamos nos atentar aos sinais. O campo não apresenta problema nenhum... nenhuma divisão por zero ou raiz de numero negativo, por exemplo. No entanto, se você for observar, temos um probleminha com a curva. Para ver se a curva é aberta ou fechada, basta ver seu valor nas extremidades de onde ela varia. Se obtivermos valores diferentes, sabemos que estamos trabalhando com uma curva aberta.
Opa, com isso conseguimoes ver que estamos trabalhando com uma curva aberta. Então vamos simplesmente fechá-la com a curva mais simples possível. Nesse caso vai ser simplesmente uma reta.
Observa que queremos simplesmente uma curva que sai do ponto A e vai para o ponto B.
Vamos então parametrizar como:
Passo 3
Dando uma olhada no sedenho da curva trabalhada no enunciado temos:
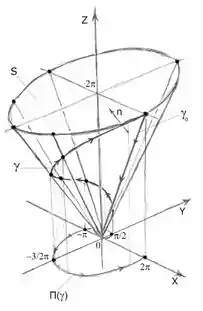
Para manter então uma orientação positiva, temos que a reta para fechar a curva aberta vai do ponto para o , então teremos da parametrização variando de para 0, e não o contrário como dito anteriormente.
Passo 4
Com isso o teorema de Stokes fica:
Resolvendo então logo a integral de linha em cima de .
Vamos precisar da parametrização da curva, o que já temos, do campo em função da parametrização e do termo .
Escrevendo o campo em função da parametrização:
Escrevendo agora o termo d
Podemos então finalmente montar a integral:
Passo 5
Partindo agora para a integral de superfície, pela figura do passo 3, observamos que a melhor superfície é um cone:
Então temos como parametrização
Como vetor normal então teremos:
Onde:
Montando então a matriz:
Escrevendo então o rotacional que achamos la no começo da resolução do exercício em função dessa parametrização ficamos com:
Montando e resolvendo então a integral:
Passo 6
Pra fechar agora basta a gente voltar pra o teorema com os resultados que encontramos.