Questão 2: Seja a superfície contida no elipsoide de equação implícita e acima do plano e seja
Um campo espacial.
- Mostre que , a curva na fronteira de , está contida na superfície de equação .
- Calcule .
- Considere que é orientada de modo que sua projeção no plano é percorrida no sentido anti-horário e calcule o trabalho do campo ao longo de .
Passo 1
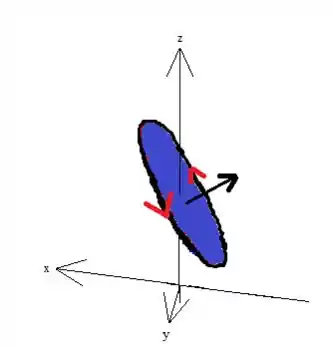
Sempre é bom ter uma noção geométrica da superfície que estamos trabalhando pra facilitar o nosso estudo. Aqui, envolve o desenho de elipsoide e de um plano que é paralelo ao eixo :
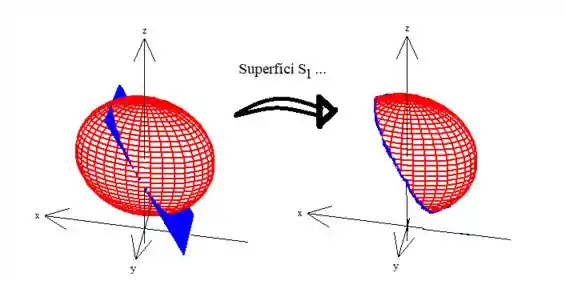
POW! Essa superfície foi desenhada graficamente no meu computador, mas eu reconheço que a gente não tem um computador na hora da prova, não é verdade? Por isso não precisa fazer um desenho perfeito, basta você entender que a superfície está em cima de um elipsoide deslocado em de unidades pra cima, e além disso, só queremos um pedaço acima de um plano paralelo ao eixo , beleza?
Passo 2
Bem, mas o que o problema na letra realmente quer, é que a gente mostre que essa curva azul aqui na borda de :
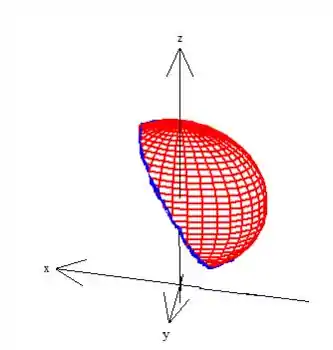
Está contida no cilindro . Para fazer essa prova, basta pegar equação do plano e do elipsoide e resolver o sistema:
VIU! De fato essa curva azul está em cima de um cilindro de raio !
Passo 3
Para o calculo do rotacional, temos que se lembrar da fórmula:
Calculando cada derivada lembrando que , e são as componentes do campo...
Derivando com atenção nas regras do produto e na regra da cadeia:
Logo, fazendo as simplificações todas...
Passo 4
Trabalho de ao longo da curva borda de é dado por uma integral de linha dessa forma aqui:
Calcular essa integral de linha de uma forma direta seria muito complicado, pois o campo não é nada fácil, além disso, já temos o rotacional calculado e vemos que ele é mais elegante que o campo . Essas dois fatos nos indica que vamos resolver a integral de linha de forma indireta pelo TEOREMA DE STOKES!
Passo 5
Por esse Teorema, temos a linda igualdade:
Onde é uma superfície que é delimitada pela curva Então, para aplicar essa igualdade temos que encontrar essa superfície!
Veja que poderíamos pegar qualquer superfície que é fechada por essa curva borda azul, inclusive poderíamos pegar o próprio pedaço de elipsoide. Porém, a gente costuma escolher a superfície mais fácil que encontramos. Nesse caso é o plano azul delimitado pelo cilindro ...
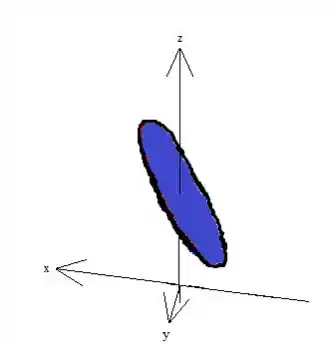
Passo 6
Outras duas condições do teorema são:
- Ter uma orientação positiva entre a superfície escolhida e a curva. Como a curva gira no sentido anti-horário pelo enunciado, devemos ter um vetor norma na superfície orientada pra cima (pela regra da mão direita):
- Outra condição diz respeito ao campo , já que esse cara não pode ter singularidades (problemas de definição) onde estamos trabalhando:
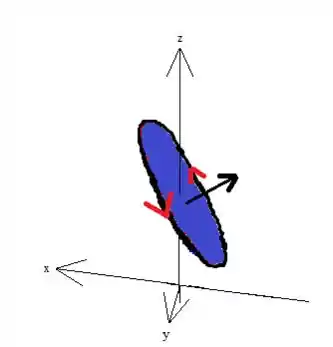
Como você mesmo pode ver, esse campo funciona em qualquer ponto que quisermos, concluindo que ele realmente não tem singularidades alguma !
Passo 7
Com essas condições estando satisfeitas, podemos retornar para o teorema de Stokes
Onde vamos calcular a integral de superfície em cima desse aqui:
OK! Então se vamos fazer isso, é melhor fazermos seguindo o método de resolução que conhecemos para integral de superfície de um campo vetorial:
- Encontrar uma parametrização para a superfície.
- Calcular .
- Encontrar o nas coordenadas da parametrização.
Então vamos nessa?
Passo 8
Uma parametrização para a superfície que está em cima de um plano , que é uma equação explícita, é um parametrização também explícita onde o e o variam livremente, enquanto está amarrado:
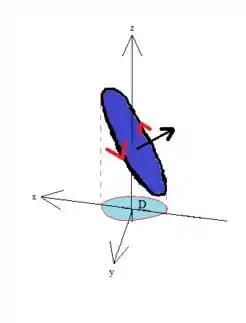
Mas o e o também não estão tão livres assim, já que sabemos que eles só podem estar dentro do cilindro de raio :
Em outras palavras: o e o variam dentro do disco no plano :
Passo 9
A segunda coisa que temos que fazer é encontrar:
Para encontrar o vetor normal a uma superfície parametrizada como gráfico de uma função dessa forma
Pode ser feito pelo Bizu:
Veja que esse vetor normal também atende a condição de termos um vetor normal apontado pra cima. Se não atendesse, bastaríamos multiplicarmos por !
Passo 10
Outra coisa que temos que fazer aqui, e a última antes de retornarmos para a integral de superfície, é encontrar o como função dos parâmetros:
Para isso, basta trocar o ...
Passo 11
Voltando para a integral de superfície então...
Veja que agora trocamos a integral de superfície pela integral dupla em cima da região . Como essa região é um disco de raio e centrado na origem:
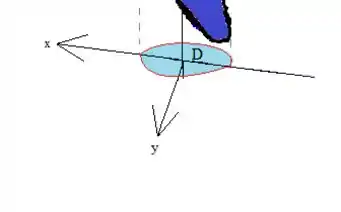
Podemos calcular a integral dupla fazendo por coordenadas polares:
Onde o Jacobiano dessa mudança vale:
Como é um disco de raio dando uma volta completa...
Logo...
Passo 12
Calculando a integral dupla...
Então pelo teorema de Stokes...