Calcule , onde e é a curva obtida como interseção da superfície , , com o plano , orientada no sentido anti-horário quando vista de cima.
Passo 1
Vamos lá, galera, essa é bem parecida com aquela que resolvemos na teoria, né? Primeira coisa que precisamos fazer é esboçar nossa curva pra entender que tipo de problema estamos lidando. A interseção do cilindro com o plano é isso aqui
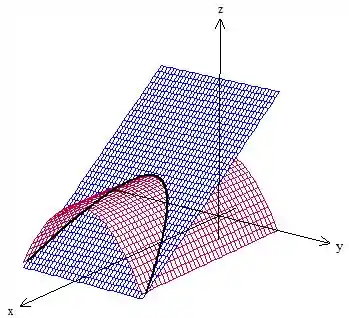
Portanto estamos lidando com uma curva aberta, o problema é que fazer essa integral diretamente seria muito trabalhoso. Vamos tentar calcular o rotacional pra ver se usar o teorema de Stokes é simples
Beleza, vamos fechar a curva com a reta que liga as duas extremidades e ver como fica o teorema de Stokes
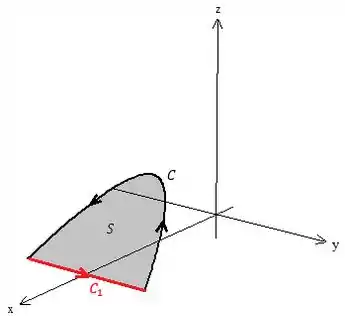
Lembre-se de tomar cuidado com as orientações das curvas! O enunciado pediu a curva com orientação anti-horária quando vista de cima, a orientação correta é essa aí do esboço. O teorema de Stokes fica
Vamos calcular então essa integral de superfície e essa integral de linha pra chegarmos na resposta final, vamos lá?
Passo 2
Como já calculamos o rotacional ali no passo 1, vamos terminar a integral dessa superfície logo. Precisamos parametrizá-la, descobrir o seu vetor normal e integrar tudo, certo? Vamos começar pela parametrização.
A superfície está toda contida no plano , sendo que somente é limitada pelo cilindro , podemos obter uma parametrização explícita pela equação do plano!
Os limites de e obtemos pela projeção da superfície no plano
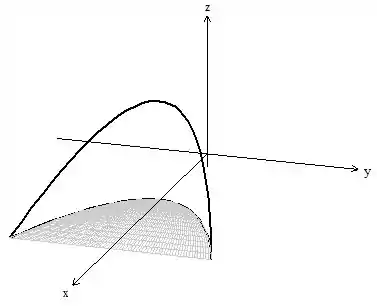
Essa parábola no plano é obtida pela interseção do plano com o cilindro
Além disso o enunciado diz que , portanto
Portanto os intervalos de e são
Graficamente dava pra perceber isso também, só não tínhamos essa equação bizarra da parábola.
Como agora temos a parametrização, vamos substituir isso no nosso rotacional
Pode estar parecendo meio bizarro, mas o produto escalar dessa cara com a normal vai facilitar um pouco as coisas, prometo!
Passo 3
A normal do plano podemos obter pelo macete de quando a parametrização é explícita, lembra dele? É isso aqui, quando
No nosso caso,
Com essa normal vamos poder zerar o termo do meio do rotacional!
Passo 4
Agora é só substituir na integral de superfície
Agora é só integrar!
Passo 5
Pronto, passou a parte mais chata, essa integral de linha agora vai ser mais tranquila. Ela é uma reta, certo? Vamos ver que pontos ela liga!
Sabemos que as extremidades dela estão no plano . Além disso, essas extremidades são limitadas por , então em uma o valor de é e em outra é . Beleza, agora falta . Podemos ver isso pela equação do plano, afinal essa reta pertence a ele!
Portanto a reta liga os pontos até e podemos parametrizá-la por
Para calcular a integral dessa reta, precisamos da derivada da sua parametrização e do campo escrito conforme o parâmetro , vamos fazer isso agora
Portanto a integral de linha fica isso aqui
Passo 6
Pronto, agora é só voltar para o teorema de Stokes