A distribuição de velocidades escalar para as moléculas de um molde certa substância é dada pela função:
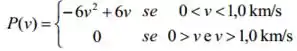
- De acordo com essa distribuição de velocidades, qual é a velocidade mais provável?
- Qual a velocidade quadrática média das moléculas?
- Tratando a substância como um gás ideal monoatômico de massa molar , calcule a temperatura da substância em para esta distribuição.
Dados:
Passo 1
a):
Bom, é uma função probabilidade. Então, a velocidade mais provável vai ser aquela que tiver a maior probabilidade em , isso é, vai ser aquela que vai gerar um pico no gráfico de
Mas como você pode ver, tem dois intervalos: de a a função é uma parábola e de pra cima o valor do gráfico é 0. Então, o gráfico com as duas partes ficará assim:
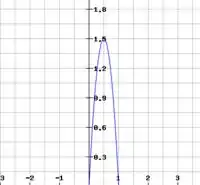
Montando o gráfico:
Basicamente só precisamos desenhar a parábola. Descobrindo as raízes:
ou
Show? São as duas raízes.
Botamos lá encima.
Dai pra achar a velocidade mais provável é só pegar a pegar a velocidade que gera o pico da parábola. Como ver isso? Bem, a o pico da parábola fica bem no meio da parábola...
Então, como as raízes são e , o pico ficará no meio delas. No caso:
E essa é a velocidade mais provável (:
Passo 2
b):
Vamos nos lembrar da relação entre a velocidade quadrática média e a a velocidade mais provável:
Então:
Passo 3
c):
Vamos usar o valor da velocidade mais provável e a formula que usa a temperatura:
Dai é só isolar
Só que esse é a massa de uma molécula. Precisamos calcular esse já que não deram pra gente. Mas como nos deram a massa molar e a constante de Avogadro:
Jogando tudo na equação:
Resposta
a):
b):
c):