A figura abaixo mostra a distribuição de probabilidade da velocidade das moléculas de uma amostra de nitrogênio. A escala do eixo horizontal é definida por . Determine a temperatura do gás e a velocidade média quadrática das moléculas.
Dado: massa molar do nitrogênio
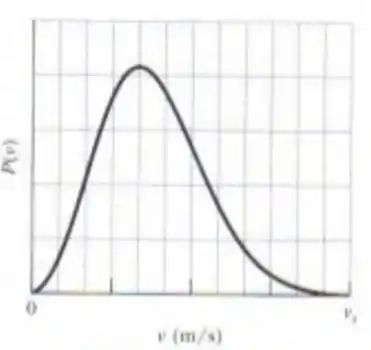
Passo 1
Par determinarmos a temperatura, precisamos descobrir qual é a velocidade mais provável, e faremos isso atráves do gráfico, a abcissa do ponto mais alto é o valor da velocidade mais provável.
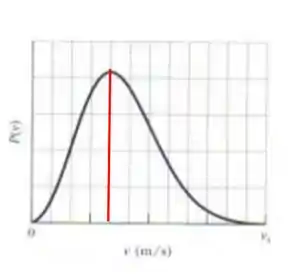
Para descobrir o ponto no eixo que a reta vermelha representa, vamos ter que descobrir quanto cada quadrado vale.
Para isso vamos dividir o valor de pela quantidade de quadrado até , assim temos
Como temos quadrados
Então como a reta vermelha está no quarto quadrado, temos que
Passo 2
Agora que sabemos a velocidade mais provável, podemos utilizar a fórmula dela para descobrirmos a temperatura
Como não sabemos a massa da amostra apenas a massa molar ,
Podemos usar que
Então
Isolando a temperatura agora, chegamos em
Substituindo pelos valores que temos
Passo 3
Para isso vamos usar a relação entre as velocidade