A figura mostra duas curvas representando possíveis distribuições esfericamente simétricas de velocidades, em três dimensões, das moléculas de uma amostra de gás segundo a distribuição de velocidades de Maxwell.
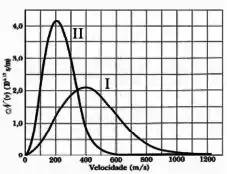
Considere as seguintes afirmativas:
A curva demonstra a situação coma temperatura mais alta.
Apesar das curvas serem diferentes, as áreas sob cada curva são iguais.
A fração de moléculas com velocidade superior à é maior para a curva
Em ambas as curvas a velocidade mais provável para uma molécula escolhida ao acaso é menor que as respectivas velocidades médias.
As afirmações corretas são:
Todas.
Passo 1
Vamos analisar cada afirmação:
- Correta, quanto maior a temperatura, mais achatada vai ser a curva!
- Correta! Essa é um pouco mais difícil de entender, mas vamos lá:
As funções de distribuição de velocidades têm no eixo , probabilidades. São funções de probabilidade, ok?
Então, são sempre números quebrados: , ,
Se quisermos calcular a área sob a curva, o que acharemos?
Acharemos a soma de todas as probabilidades da amostra! E qual é a soma de todas as probabilidades? , ou 1!
Então, não importa o formato da curva, sempre dará 1. Ou, matematicamente:
Onde é a função de distribuição das probabilidades.
Passo 2
- Essa é bem tranquila. Dê uma olhada no gráfico. Achou o ponto que tem velocidade
Então, trace um linha vertical assim:
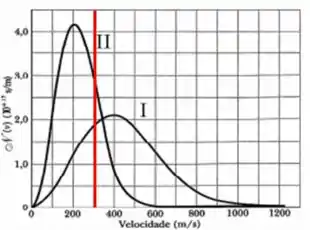
Agora veja a área abaixo do gráfico 2 e a área abaixo do gráfico 1, analisando apenas as partes dos gráficos que estão depois da linha vermelha.
Como vimos, a área sob o gráfico nos dá a probabilidade total. Como a área de 2 é menor que a área de 1, a probabilidade total também de 2 também é menor.
Uma probabilidade maior acaba levando a um maior número de moléculas, então, essa afirmativa é falsa. Na verdade, a fração maior pertence ao gráfico 1.
Passo 3
- Verdade! Basta olhar na nossa teoria a relação entre a velocidade mais provável de um gás e a sua velocidade média. A relação é:
Como
Então a velocidade mais provável de uma molécula de um gás é sempre menor que a sua velocidade média.