As cinco primeiras repetições de um experimento custam $10,00 cada. Todas as repetições subsequentes custam $5,00 cada. Suponha que o experimento seja repetido até que o primeiro sucesso ocorra. Se a probabilidade de sucesso de uma repetição é igual a 0,9, e se as repetições são independentes, qual é o custo esperado?
Passo 1
Vamos analisar o enunciado e ver se estamos falando de alguma distribuição? Bom o enunciado diz que temos um experimento onde temos duas fatores a serem analisados:
-X: O número de tentativas
- C: O custo dos experimentos
Sabemos que iremos realizar o experimento até que o primeiro sucesso ocorra ou seja, temos uma Distribuição Geométrica certo?
Passo 2
Agora que já sabemos qual é o modelo vamos entender o que cada coisa é... Se tentamos até conseguir o primeiro sucesso, todas as tentativas anteriores são de fracasso (não sucesso). Ou seja, se tentamos num total de X tentativas, teremos 1 sucesso e fracassos. Considere:
- Probabilidade de Sucesso:
- Probabilidade Não Sucesso:
Juntando tudo podemos escrever:
Substituindo os valores do enunciado:
Passo 3
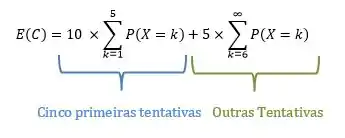
O enunciado pede o custo esperado, simbora calcular? O cálculo do custo é feito da seguinte forma:
- 5 primeiras tentativas : R$10,00 cada
- Outras tentativas: R$5,00 cada.
Assim podemos escrever que:
Passo 4
Agora é só substituindo e ir para as contas!