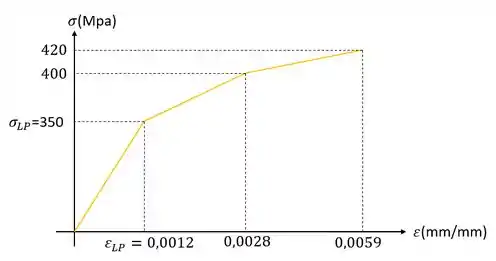
Com base no gráfico de tensão e deformação dado abaixo, determine o módulo de resiliência e de tenacidade desse material.
Passo 1
Para resolver esse exercício precisamos relembrar como determinar o modulo de resiliência e de tenacidade usando um gráfico de tensão por deformação. Vamos começar pelo modulo de resiliência.
O modulo de resiliência é calculado pela fórmula
Em que são valores de tensão e deformação no limite de proporcionalidade. Se prestarmos atenção essa fórmula representa exatamente a área do primeiro triangulo que aparece na nossa figura, que representamos na imagem abaixo
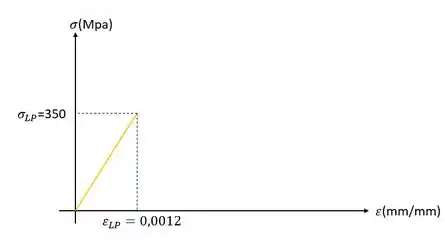
Passo 2
Já sabemos o que fazer com o modulo de resiliência, mas e o modulo de tenacidade?
O modulo de tenacidade é bem tranquilo, é só determinar a área abaixo do gráfico, como mostrado a seguir
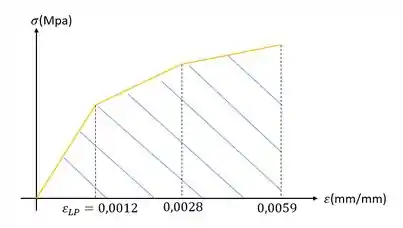
Passo 3
Agora que já sabemos como calcular cada um desses valores, vamos determina-los.
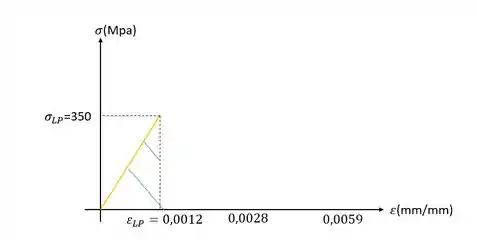
Primeiro o modulo de resiliência.
Sabemos que
Como a fórmula é
Substituindo teremos que
Como queremos uma unidade de densidade de energia, multiplicaremos em cima e embaixo por metros, teremos então
Passo 4
Precisamos determinar também o modulo de tenacidade, e para isso precisamos calcular a área abaixo do nosso gráfico, vamos dividir então o nosso gráfico em três regiões de interesse.
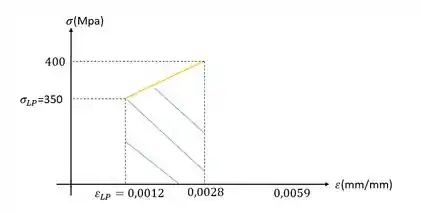
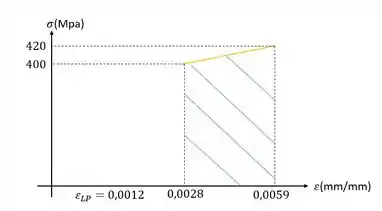
Agora basta calcularmos a soma dessas áreas para definirmos o modulo de tenacidade do nosso material.