O pilar abaixo está submetido ao carregamento mostrado. Usando seus conhecimentos acerca de energia de deformação, determine o valor da energia de deformação dessa peça.
.
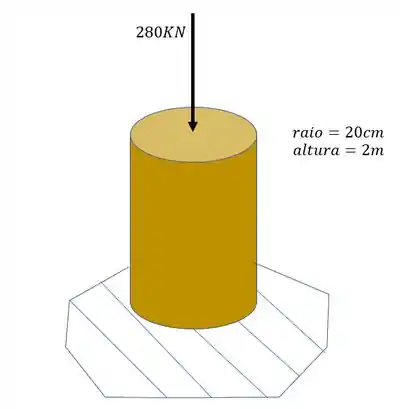
Passo 1
Esse exercício quer testar o nosso cuidado com unidades e aplicação de fórmula, então vamos tomar alguns cuidados nas nossas resoluções. Vamos primeiro determinar a fórmula que devemos usar.
Em que sabemos que podemos determinar cada termo dessa equação pelas fórmulas
Em que a área é
Sabemos também que podemos definir a deformação especifica pela lei de Hooke da seguinte maneira
E por fim sabemos que o volume nesse caso se trata do volume do cilindro que é dado por
Passo 2
Como já temos as nossas fórmulas, vamos substitui-las na equação principal.
Passo 3
Vamos agora substituir os valores que o enunciado nos dá e vamos determinar o valor da nossa energia
Calculando a energia teremos que