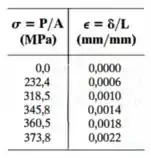
Os dados obtidos em um ensaio de tensão-deformação para um material cerâmico são dados na tabela. A curva é linear entre a origem e o primeiro ponto. Represente o diagrama em gráfico e determine o módulo de elasticidade e o módulo de resiliência.
Passo 1
A primeira coisa que fazemos nesse exercício é desenhar o Diagrama Tensão-Deformação do material em um gráfico:
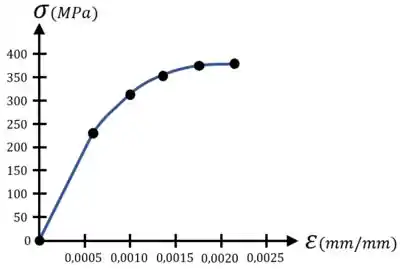
Em seguida, o exercício quer que a gente determine o módulo de elasticidade e o módulo de resiliência desse material.
Para tanto, vamos usar a informação de que a curva é linear entre a origem e o primeiro ponto.
O que isso significa é que o primeiro ponto é o limite de proporcionalidade do material (o último ponto do diagrama que segue a Lei de Hooke), de tal forma que:
Agora, lembra aí!
Para calcular o módulo de elasticidade de um material, podemos usar os valores de e de qualquer ponto do diagrama tensão-deformação que siga a Lei de Hooke .
Usando e , vamos ter que:
O que significa que:
E para calcular o módulo de resiliência do nosso material, podemos nos lembrar que ele é igual à área triangular debaixo da região linear do diagrama tensão-deformação:
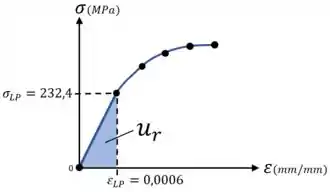
Ou podemos nos lembrar diretamente da fórmula para :
Passo 2
Agora que já desenhamos o Diagrama Tensão-Deformação do material e entendemos como encontrar os valores de e para o material, vamos calcular esses valores!
Para o módulo de elasticidade , temos que:
Substituindo os valores de e , encontramos que:
O que dá:
Como esse número é um pouco grande, o reescrevemos em :
E para o módulo de resiliência , temos que:
Substituindo os valores de e , encontramos:
Calculando, isso dá:
Passo 3
Poderiamos já terminar o exercício por aqui.
Mas temos mais uma coisa que podemos fazer: como é uma medida de densidade de energia, queremos dar o resultado de em uma unidade de energia sobre volume.
(A unidade atual do nosso resultado para é , que é uma unidade de tensão!)
Então vamos pensar...
Multiplicando em cima e em baixo por , isso fica assim:
Mas é o mesmo que joule, então:
Sendo assim, podemos reescrever o nosso resultado, que está em , em :
E assim, finalizamos o exercício: