A água escoa através de um tubo que possui uma redução responsável por reduzir o diâmetro para do seu tamanho inicial.
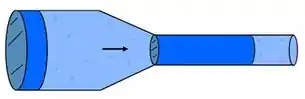
Se a velocidade da água na seção maior do tubo é de , qual será a sua velocidade nesta seção menor?
Passo 1
Quase terminando em galerinha, forçaa!!
O que temos é o seguinte, um fluido está escoando sobre um tubo com diâmetro grande, , até que ocorre uma redução de desse diâmetro .
Vamos escrever essa relação entre os diâmetros. Lembrando que podemos escrever qualquer porcentagem como uma divisão por , então
Show! Agora sabemos como escrever em “matematiques” que o diâmetro fica do diâmetro
Vamos guardar essa relação que vai ser importante!
Passo 2
Bom, se queremos achar a velocidade na seção menor podemos usar a equação da continuidade:
Isolando a velocidade neste ponto , a área vai para o outro lado dividindo:
A área da secção transversal do cilindro é dada por:
Chegou o momento de usar aquela relação das diagonais que encontramos no passo !
Substituindo essas áreas na fórmula que encontramos para a velocidade
Nossa, essa relação ficou feia demais! hehe. Mas podemos fazer umas simplificações. Repare que tem um em cima e em baixo, podemos cortar e elevar todo mundo que está dentro dos parênteses ao quadrado
Bem... ainda não ajudou muito, né!? Mas ainda dá para cortar mais coisas aí. Vamos linchar aquele que está em cima e em baixo
Olha como ficou mais bonito, dá até um alívio no coração, não é? Vamos só elevar aquele ao quadrado agora
Passo 3
Sabemos também que a velocidade no ponto é:
Então:
O que acharam desta?!