Um carpinteiro monta uma marquise de madeira de de comprimento e massa em uma parede de uma loja. A marquise é presa por um pino na parede e por um cabo de aço com de comprimento. O cabo e preso na parede a acima do pino e na marquise a do pino. Despreze a massa do cabo. O sistema esta em equilíbrio. .

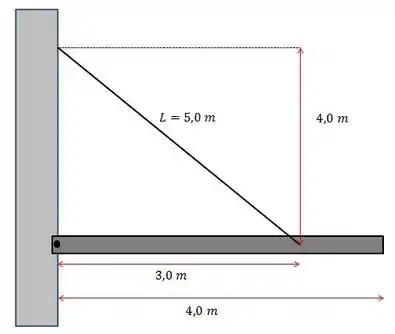
a) Determine o vetor tensão no cabo.

b) Determine o vetor força que age no pino devido a marquise.

c) Para testar a estrutura depois de pronta, o carpinteiro se pendura na sua borda. Sabendo

que a tensão máxima que o cabo de aço suporta é de , determine qual a maior massa que o carpinteiro pode ter para que o cabo não arrebente durante o teste. Considere o carpinteiro como uma massa pontual.

Vamos marcar as forças que estão atuando aí no nosso desenho.

Algumas observações importantes:

A marquise tem massa e tá sujeita a atração gravitacional da Terra, então temos o peso.

O fio não tem massa, então não temos o peso do fio;

Temos um fio, então temos uma tração/tensão no fio;

A marquise tá apoiada num pino, então tem uma força que o pino exerce na marquise. Pra gente entender bem a direção da força, vamos fazer um experimento...

Tenta segurar o seu celular só com o dedão e o dedo indicador e tenta manter o celular na horizontal, mais ou menos assim:

Desenhando as nossas forças, coloquei um ângulo ali entre o fio e a horizontal, só pra ficar mais fácil depois, e na figura do lado eu juntei todas as forças em um ponto só:

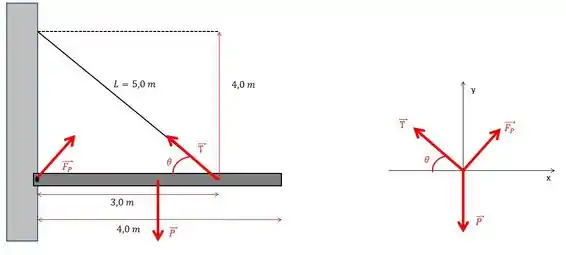
Agora vamos usar as condições de equilíbrio para as forças na direção e .

Mas reparem que a gente não sabe nada sobre a força que o pino exerce. Então essas condições de equilíbrio não foram muito legais pra esse problema. (Mas elas são uteis para outras problemas, então é bom entender direitinho)

Bom, agora vamos para a última condição de equilíbrio, que o o torque resultante em relação ao pino ser zero.

Como está em cima do nosso ponto de apoio,

Para o torque da tração:

Lembrando que é o vetor que vai do ponto do eixo de rotação (pino) até o ponto de aplicação da força:

Resolvendo o produto vetorial:

Sabemos que . Pra calcular o é só olhar pro triângulo retângulo que o fio forma com a parede e a marquise:

Substituindo:

Beleza, guarda essa aí.

Vamos agora calcular o torque a força peso exerce no pino:

Agora o vetor distância vai ser diferente, porque o peso é aplicado no meio da barra!

Calculando o produto vetorial:

E substituindo os valores:

Agora, vamos usar esses valores la na equação de condição de equilíbrio:

Maravilha, essa é a intensidade do vetor tração.

Pra gente achar de fato o vetor, temos que dar suas direções, então vamos usar:

Mas quem é o nosso e

Vamos olhar lá na figura:

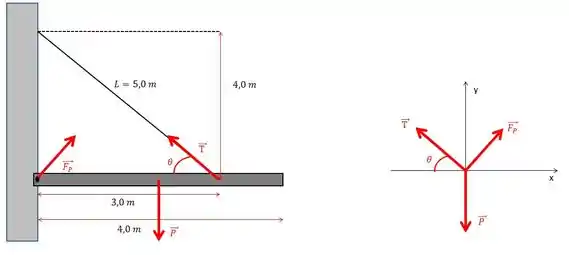
Já calculei o seno e o cosseno olhando pra figura da esquerda.

Então:

Show!

(b)

Agora ele quer saber . Como já sabemos , ficou moleza.

É só usar aquelas equações da condição de equilíbrio para a força resultante ser zero:

Substituindo , que achamos na letra a:

Para as forças em y:

Substituindo e Mg:

Então o vetor

Maravilha! Vamos pra letra c.

(c)

Agora o carpinteiro se pendura na borda da marquise:

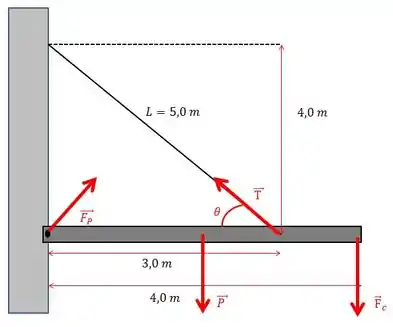
Eita, essa força que o carpiteniro faz, gera um torque novo no nosso pino.

Como queremos que a marquise fique no lugar, a condição de equilíbrio ainda vale:

Vamos ver quanto vale o torque que o carpinteiro produz:

Substituindo os valores:

Como queremos saber a massa que o carpinteiro tem para que a tensão seja máxima, vamos o usar seu valor máximo:

Portanto o

Resolvendo o produto vetorial:

Substituindo os valores:

Beleza, substituindo esses valores lá na equação de equilíbrio:

Ajeitando isso:

Portanto a maior massa possível para o carpinteiro é .