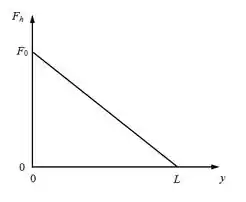
A figura mostra uma viga vertical uniforme de peso e comprimento , presa a uma dobradiça na extremidade inferior. Uma força horizontal de módulo constante é aplicada a uma altura
. Na extremidade superior, a viga está presa a um cabo que faz um ângulo com a horizontal.
Determine a tensão no cabo em termos de .
Seja o módulo da componente horizontal da força que a dobradiça exerce sobre a viga.
Esboce o gráfico da função no intervalo , indicando claramente os valores de e .
Passo 1
A viga está em equilíbrio e por isso podemos aplicar a 2ª Lei de Newton e dizer que e ainda por estar em equilíbrio também podemos usar a equação
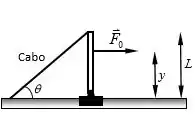
Então o primeiro passo em uma questão desse tipo é fazer o diagrama de força. As forças atuantes são: e :
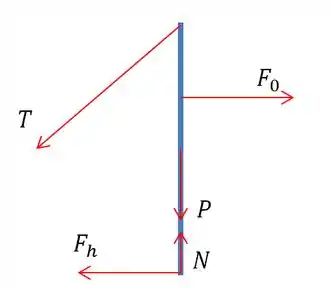
Porém precisamos decompor a tensão, para que todas estejam no eixo ou .
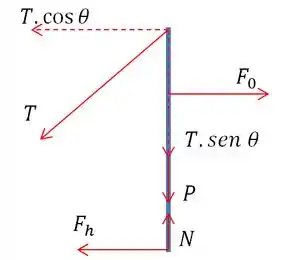
Agora faremos o equilíbrio de forças no eixo .
Fazendo o mesmo para o eixo :
Como o item pede que a tensão no cabo seja dada apenas por e , não podemos usar as equações acima, pois não sabemos o valor da Normal, nem de . Então teremos que usar o momento em relação a dobradiça, pois assim sumimos com a força e conseguiremos calcular a Tensão no cabo.
Fazendo , temos
Show de bola, conseguimos uma equação onde conhecemos todas as incógnitas, exceto que é o que queremos. Isolando a tensão chegamos em:
Passo 2
Queremos esboçar um gráfico mostrando o valor da força . Então para isso o primeiro passo é descobrir a equação dessa força.
Agora que já temos a tensão, fazer isso é fácil, basta substituirmos o valor de na equação de equilíbrio (força) no eixo :
Substituindo , temos:
Isolando :
Essa equação é linear, certo? Se você se esqueceu, linear é quando só há termos de primeira ordem na equação, tipo .
Sendo linear, essa equação representa uma reta. Então basta marcamos dois pontos que teremos a reta determinada e assim será moleza fazer o gráfico.
Os pontos o problema já falou qual escolheremos: e . Primeiro descobriremos quando :
E agora descobrindo o outro ponto:
Marcando os dois pontos e traçando a única reta possível, temos:
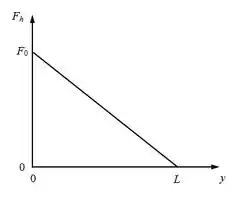
Repara aqui que como ele quer a força em função de y, colocamos o y no eixo horizontal (porque ele é a variável independente) e a força no eixo vertical.
Resposta