O sistema da figura abaixo está em equilíbrio, com a corda do centro exatamente na horizontal. O bloco A pesa 40 N, o bloco B pesa 50 N e o ângulo é 35°.
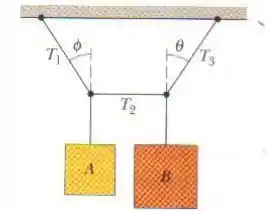
Determine:
- A tensão ,
- A tensão ,
- A tensão ,
- O ângulo .
Passo 1
a)
Analisando as forças no bloco A, montamos o seguinte diagrama:
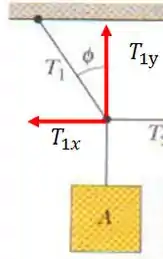
Como o sistema está em equilíbrio:
Passo 2
b)
Montando o diagrama abaixo:
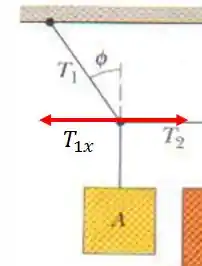
Para o sistema estar em equilíbrio:
Passo 3
c)
Montando o diagrama no ponto que passa:
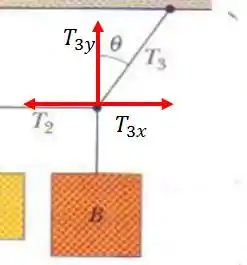
Já a componente de será o peso do bloco que pelo enunciado é , ou seja
é a resultante de e , logo:
Passo 4
d)
Para achar o valor do ângulo , basta calcular a .
Pega uma calculadora aí, e você vai achar que:
Resposta
- 49 N
- 28 N
- 57 N
- 29°
Exercícios de Livros Relacionados
Na Figura um pacote de massa m está pendurado em uma corda que, por sua vez, está presa à parede através da corda 1 e ao teto através da corda 2 . A corda 1 faz um ângulo φ = 40 ° com a horizontal; a
A figura mostra uma viga vertical homogênea de comprimento L que está presa a uma dobradiça na extremidade inferior. Uma força horizontal F a é aplicada à viga a uma distância y da extremidade inferio
Na figura, uma caçamba de 817k g está suspensa por um cabo A que, por sua vez, está preso no ponto 0 a dois outros cabos, B e C , que fazem ângulo θ 1 = 51,0 ° e θ 2 = 66,0 ° com a horizontal. Determi
Na figura, um andaime horizontal, de 2,00 m de comprimento e massa homogênea de 50,0k g está suspenso de um edifício por dois cabos. O andaime tem várias latas de tinta empilhadas. A massa total das l
Na figura, suponha que o comprimento L da barra uniforme seja 3,00m e seu peso seja 200N . Suponha ainda que o bloco tenha um peso P=300N e que θ=30,0 ° . O fio pode suportar uma tensão máxima de 500N