Na figura abaixo, uma caçamba de 817 kg está suspensa por um cabo A que está preso no ponto O a dois outros cabos, B e C, que fazem ângulos e com a horizontal. Determine as tensões: Sugestão: Para não ter que resolver um sistema de duas equações com duas icógnitas, defina os eixos da forma mostrada na figura.
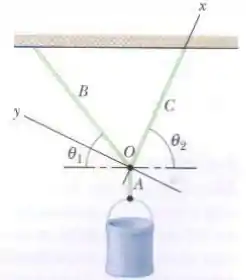
- No cabo A,
- No cabo B,
- No cabo C.
Passo 1
No cabo A, chegamos à conclusão que:
Passo 2
b) Vamos utilizar os eixos conforme sugerido no enunciado:
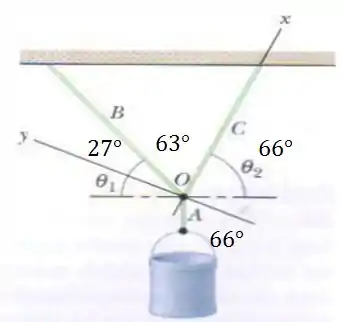
Para o sistema estar em equilíbrio:
Passo 3
Para estar em equilíbrio, o somatório de forças no eixo x também deve ser igual a zero.
Resposta
- 8006 N
- 3654 N
- 5654 N
Exercícios de Livros Relacionados
Na Figura um pacote de massa m está pendurado em uma corda que, por sua vez, está presa à parede através da corda 1 e ao teto através da corda 2 . A corda 1 faz um ângulo φ = 40 ° com a horizontal; a
A figura mostra uma viga vertical homogênea de comprimento L que está presa a uma dobradiça na extremidade inferior. Uma força horizontal F a é aplicada à viga a uma distância y da extremidade inferio
Na figura, uma caçamba de 817k g está suspensa por um cabo A que, por sua vez, está preso no ponto 0 a dois outros cabos, B e C , que fazem ângulo θ 1 = 51,0 ° e θ 2 = 66,0 ° com a horizontal. Determi
Na figura, um andaime horizontal, de 2,00 m de comprimento e massa homogênea de 50,0k g está suspenso de um edifício por dois cabos. O andaime tem várias latas de tinta empilhadas. A massa total das l
Na figura, suponha que o comprimento L da barra uniforme seja 3,00m e seu peso seja 200N . Suponha ainda que o bloco tenha um peso P=300N e que θ=30,0 ° . O fio pode suportar uma tensão máxima de 500N