(Adaptado) Um arranjo de tubos concêntrico, para o qual os diâmetros interno e externo são e , respectivamente, é usado para remover calor de uma reação bioquímica ocorrendo em um tanque de repouso.
Calor é gerado uniformemente no interior do tanque a uma taxa de e uma vazão de de água é alimentada na região anular.
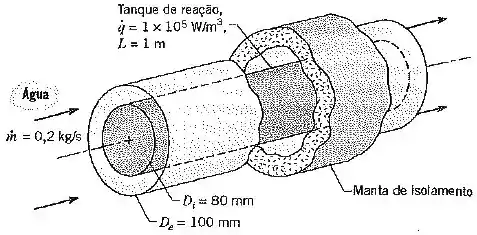
Determine a temperatura de entrada da água vinda do suprimento que irá manter uma temperatura da superfície do tanque média de . Suponha escoamento e condições térmicas plenamente desenvolvidas.
Utilize as seguintes propriedades para a água:
Passo 1
O drama aqui é que não temos nem a temperatura de entrada e nem a de saída , então precisamos dar um jeito de encontra-las.
Bom, a taxa de calor transferida para a água é dada por:
O problema nos deu o calor gerado na superfície interna, e sabemos que a superfície externa é termicamente isolada .
Dessa forma, a taxa de transferência de calor será:
Ao mesmo tempo, podemos associar a taxa de transferência de calor entre o fluido e a superfície interna da seguinte forma:
Onde ..
Opa! Então podemos encontrar a temperatura média reorganizando a equação acima:
Ao encontrarmos a temperatura média, podemos encontrar as temperaturas de entrada e saída reorganizando a primeira equação que vimos:
Ou seja, precisamos do danado do coeficiente convectivo na superfície interna .
Passo 2
Começando pelo número de Reynolds, temos que:
Onde:
Substituindo na expressão do número de Reynolds:
Opa! Estamos no regime laminar! Como estamos trabalhando em um caso onde há fluxo térmico na superfície interna , e uma superfície externa termicamente isolada , temos que:
Logo:
Finalmente, o coeficiente convectivo será:
Passo 3
A temperatura média será:
Passo 4
Agora que já temos a temperatura média, podemos encontrar a temperatura de entrada da seguinte forma:
Substituindo isso na expressão abaixo, teremos:
Agora é só arrumar a bagunça.
Substituindo os valores:
![]()