É prática comum recuperar calor em fornalhas que queimam óleo ou gás através da utilização dos gases de exaustão no preaquecimento do ar de combustão.
Um dispositivo normalmente utilizado para esse propósito é composto por um arranjo de tubos concêntricos no qual os gases de exaustão escoam no tubo interno e o ar de combustão, mais frio, escoa pela região anular.
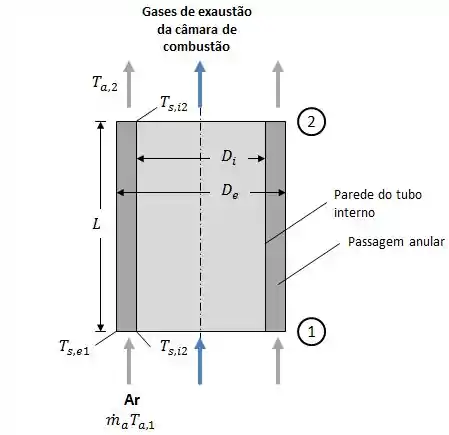
Considere condições nas quais há uma taxa de transferência de calor uniforme por unidade de comprimento do tubo, , dos gases de exaustão para a superfície interna do tubo interno, enquanto o ar escoa pela passagem anular a uma vazão de .
O tubo interno, com parede delgada, tem diâmetro , enquanto o tubo externo, que está isolado da vizinhança, possui diâmetro . As propriedades do ar podem ser consideradas iguais a , , e .
Se o ar entra no arranho a e , qual é a temperatura do ar na saída ?
Se o escoamento do ar é plenamente desenvolvido ao longo de toda a região anular, qual é a temperatura do tubo interno nas seções de entrada e de saída do arranjo? Qual é a temperatura do tubo externo na entrada do arranjo ?
Passo 1
Se o ar entra no arranho a e , qual é a temperatura do ar na saída ?
Como o problema já nos deu as propriedades do ar, podemos determinar a temperatura de saída do ar da seguinte forma:
Substituindo os valores, teremos:
![]()
Passo 2
Se o escoamento do ar é plenamente desenvolvido ao longo de toda a região anular, qual é a temperatura do tubo interno nas seções de entrada e de saída do arranjo? Qual é a temperatura do tubo externo na entrada do arranjo ?
A temperatura superficial é será dada por:
Ou seja, precisamos determinar o coeficiente convectivo pra cada caso, beleza?
Passo 3
Para calcular os coeficientes convectivos, precisamos do número de Nusselt, já que:
Para calcular o número de Nusselt, precisamos do número de Reynolds, dado por:
Onde:
Substituindo os valores:
Opa! Como , estamos no regime turbulento.
Passo 4
Como estamos no regime turbulento, o número de Nusselt será o mesmo tanto para a superfície interna, quanto para a superfície externa, e será dada por:
Substituindo os valores:
Os coeficientes convectivos nas superfícies interna e externa serão:
Agora já podemos determinar as temperaturas que o problema pede.
Passo 5
Como vimos lá no Passo 1, a temperatura de qualquer ponto da superfície é dada por:
- Temperatura do tubo interno nas seções de entrada :
- Temperatura do tubo interno nas seções de saída :
- Temperatura do tubo externo na entrada do arranjo :
Como estamos trabalhando na seção de entrada:
Onde:
Logo:
![]()
Passo 4
Agora, como estamos trabalhando na seção de saída:
Onde:
Logo:
![]()
Passo 5
Como não temos fluxo térmico na superfície externa:
![]()
Resposta