Os gases de exaustão de um forno de processamento de fios são descarregados em uma grande chaminé e as temperaturas do gás da superfície na saída da chaminé devem ser estimadas.

O conhecimento da temperatura de saída do gás é útil para estimar a dispersão dos efluentes na pluma térmica, enquanto o conhecimento da temperatura da superfície de saída da chaminé indica se irá ocorrer a condensação dos produtos gasosos.

A chaminé cilíndrica e com parede delgada possui de diâmetro e de altura. A vazão dos gases de exaustão é de e a temperatura de entrada dos gases é de .

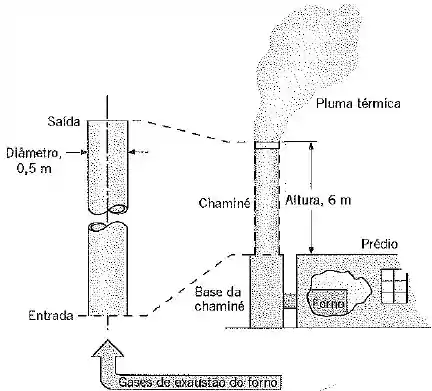
Considere condições nas quais a temperatura do ar ambiente, a velocidade do vento e o coeficiente convectivo externo são de e , respectivamente. Aproximando as propriedades termofísicas do gás por aquelas do ar atmosférico, estime as temperaturas de saída do gás e da superfície da chaminé em sua saída para as condições dadas.

A temperatura média de saída dos gases será dada pela seguinte equação:

Onde corresponde ao coeficiente global de transferência de calor, podendo ser calculado da seguinte forma:

Já para a temperatura na superfície na saída dos gases, podemos pensar o seguinte: o fluxo de calor deve ser igual para a convecção interna e para a convecção externa, logo:

Ou seja, encontramos a temperatura média de saída, e depois encontramos a temperatura na superfície de saída.

De qualquer jeito, vamos precisar primeiro do coeficiente convectivo interno , então vamos atrás dele.

O coeficiente convectivo interno é dado por:

Para calcular o número de Nusselt vamos precisar calcular o número de Reynolds, dado por:

Como o escoamento é turbulento, e considerando , teremos:

Dessa forma, o coeficiente convectivo interno será:

Dessa forma, a temperatura média de saída será:

Onde:

Substituindo os valores:

Assim, a temperatura na superfície de saída será dada por:

Reorganizando os termos: