A figura abaixo mostra uma pequena lâmpada pendurada a uma distância acima da superfície da água de uma piscina na qual a profundidade da água é . O fundo da piscina é um espelho.
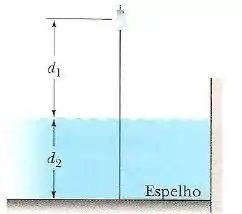
A que distância da superfície do espelho está a imagem da lâmpada?
(Sugestão: Construa um diagrama de dois raios, mas leve em conta o desvio dos raios luminosos causado pela refração. Suponha que os raios não se desviem muito de uma reta vertical passando pela lâmpada e use a aproximação, válida para pequenos ângulos, de que .)
Passo 1
Fazendo exatamente as mesmas considerações que fizemos na teoria, chegaremos à seguinte fórmula:
Onde:
Logo:
Resposta
Exercícios de Livros Relacionados
Uma vela com 4,85 cm de altura está a uma distância de 39,2 cm do lado esquerdo de um espelho plano. Onde a imagem se forma e qual é sua altura?
Você tem 1,62 m de altura e deseja ver sua imagem completa em um espelho plano vertical.a) Qual é a altura mínima do espelho que atende à sua necessidade?b) A que distância acima do solo deve estar a
Mostre que a equação dos espelhos (Equação 32-4 onde f = r / 2 ) fornece a distância imagem correta e a ampliação para um espelho plano.
a) Dois espelhos planos fazem um ângulo de 90 ° . A luz de um objeto puntiforme que está posicionado arbitrariamente na frente dos espelhos produz imagens em três posições. Para cada posição da imagem
A figura mostra uma vista de topo de um corredor com um espelho plano M montado em uma das extremidades. Um ladrão B se esgueia por um corredor em direção ao centro de um espelho. Se d = 3,0m , a que