Prove que se um espelho plano for girado de um ângulo o raio refletido girará de um ângulo . Mostre que esse resultado é razoável para .
Passo 1
A situação é basicamente essa:
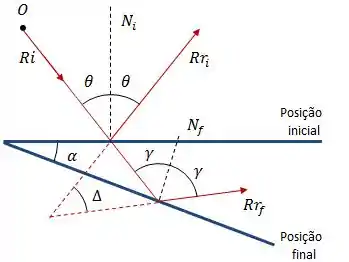
Onde é o ângulo de rotação do raio refletido.
Passo 2
Um detalhe importante e que pode ser que não seja muito nítido é a relação entre os ângulos , e , que é dada por:
A partir disso, vamos analisar o triângulo formado pelos prolongamentos dos raios refletidos:
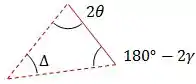
A soma dos ângulos internos de um triângulo deve ser sempre igual a , logo:
Reorganizando isso, teremos:
Onde :
Passo 3
Assim, se o ângulo de rotação for de , o raio refletido girará em .
Para mostrar que é razoável, vamos começar imaginando a situação em que o raio incide sobre uma superfície com um ângulo de incidência inicial de .
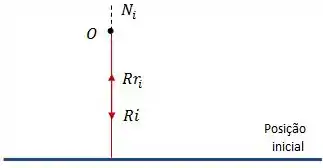
Agora vamos ver o que acontece quando giramos o espelho em .
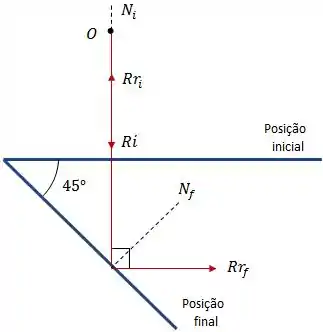
Como podemos ver na imagem acima, o raio refletido final teve uma rotação de em relação ao raio refletido inicial.
Resposta
Ei, a resposta está no passo a passo :)