A figura abaixo é uma vista de topo de dois espelhos planos verticais com um objeto entre eles.
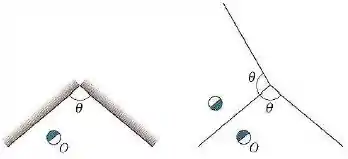
Quando um observador olha para os espelhos vê múltiplas imagens do objeto. Para determinar as posições dessas imagens desenhe o reflexo em cada espelho da região entre os espelhos, como foi feito para o espelho da esquerda na figura da direita.
Em seguida, desenhe o reflexo do reflexo. Continue da mesma forma do lado esquerdo e do lado direito até que os reflexos se cruzem ou se superponham do lado de trás dos espelhos. Quando isso acontecer, basta contar o número de imagens de .
Determine o número de imagens formadas para ; ; .
Para , determine o menor e o maior número de imagens que podem ser observadas, dependendo do ponto de vista do observador da posição do objeto .
Para cada situação, indique as posições e orientações de todas as imagens de em um desenho semelhante ao da figura acima.
Passo 1
Determine o número de imagens formadas para .
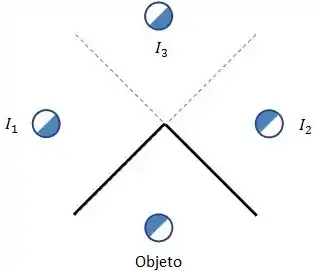
Outra forma de resolver o problema é aplicando a seguinte equação:
Para :
Passo 2
Determine o número de imagens formadas .
Para :
Passo 3
Determine o número de imagens formadas .
Para :
Passo 4
Para , determine o menor número de imagens que podem ser observadas, dependendo do ponto de vista do observador da posição do objeto .
Para o número total de imagens formadas é dada por:
Assim, se o observador olhar o sistema de modo que ele, o objeto e uma das imagens estejam na mesma linha, ele só poderá ver .
Passo 5
Para , determine o maior número de imagens que podem ser observadas, dependendo do ponto de vista do observador da posição do objeto .
O número máximo de imagens que podem ser observadas é justamente e o número de imagens formadas. Nesse caso, .
Resposta