Uma pessoa de deseja ver a imagem de seu corpo inteiro em um espelho plano. O espelho deve ter um comprimento mínimo de:
nenhuma das respostas acima: a resposta depende da distância da pessoa ao espelho.
Passo 1
Vamos imaginar a pessoa se olhando no espelho.
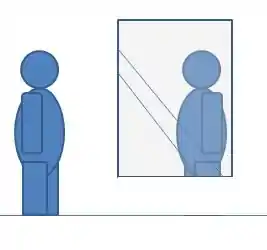
Para sabermos o que uma pessoa deve ver num espelho plano, o que nós fazemos é traçar retas dos seus olhos passando pelos extremos do espelho. Então, vamos abstrair um pouco o desenho acima, e teremos:
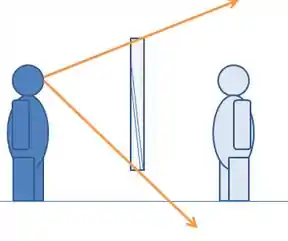
Ela conseguirá enxergar tudo que estiver entre as duas setas. Para enxergar sua própria cabeça então, o espelho precisará estar pelo na altura da cabeça, com a seta de cima batendo na cabeça. Além disso, para estar no limite de conseguir enxergar os pés, a seta de baixo deve ir de seus olhos até os pés da imagem.
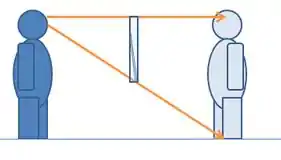
Ok, para ela se enxergar completamente no espelho, é preciso que aconteça como na imagem acima!
Passo 2
As setas e a imagem da pessoa formam um triângulo grande, e as setas com o espelho formam um triângulo pequeno. Além disso, a distância da pessoa até o espelho será igual à distância de sua imagem até o espelho. Sendo assim, teremos, colocando as dimensões na imagem:
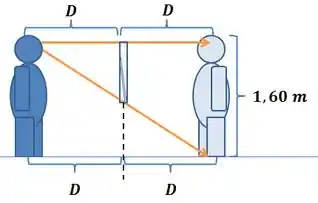
Os dois triângulos que eu mencionei, ambos são triângulos retângulos com todos os seus ângulos iguais! (Na figura, o espelho é paralelo à imagem, à direita, e por isso o ângulo que a seta de baixo faz com os dois é igual).
Assim, eles são semelhantes, e podemos fazer uma regra de três entre seus lados. Sendo o tamanho do espelho plano, temos os dois triângulos:
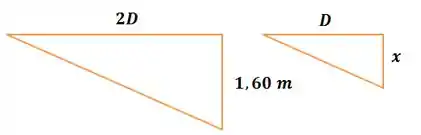
De para , nós dividimos por . Logo, por regra de três:
O que corresponde à alternativa .
Resposta
Alternativa