Seja uma amostra aleatória extraída de uma população com função densidade da forma:

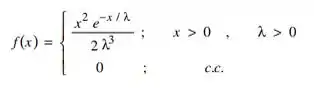
Identifique o estimador de máxima verosimilhança do parâmetro desconhecido, com base na amostra aleatória.

Agora calculamos a função , dada por:

Lembrando que os índices vão no . Abrindo issaê:

Por enquanto mantemos esse produtório aí mesmo, já que não dá pra reescrevê-lo de nenhuma outra forma.

Agora aplicamos logaritmo natural na função que calculamos no passo anterior:

Temos três produtos dentro desse logaritmo, vamos separá-los usando a propriedade dos produtos do logaritmo:

Acabamos de falar da propriedade do produto, certo? Então vamos usá-la aqui de novo no produtório, que nada mais é que um produto vezes. Se o logaritmo do produto é igual a soma dos logaritmos...

Então reescrevendo nossa função com essa substituição e usando a propriedade dos expoentes no logaritmo pra derrubar os expoentes:

Como :

Agora derivamos o que acabamos de achar, em relação ao parâmetro desconhecido :

A derivada da soma é igual a soma das derivadas, então...

Podemos reparar que o segundo termo não tem , então a derivada dele vai ser zero.

Derivando o primeiro termo separadamente:

Queee? Tendi nada! Aqui nós fizemos a regra da cadeia das derivadas! Primeiro derivamos o como se fosse a derivada de , ou seja:

E depois multiplicamos o resultado pela derivada do , que vale:

Agora derivando o terceiro termo separadamente:

Então, juntando todos os termos, nossa derivada fica:

Agora igualamos essa derivada a zero para achar o estimador:

Multiplicando tudo por :

Isolando o :

Mas sabemos que , certo? É a fórmula da nossa média amostral, então: