Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Equação da Continuidade

Ver Teoria
Exercício 12345678

Enunciado

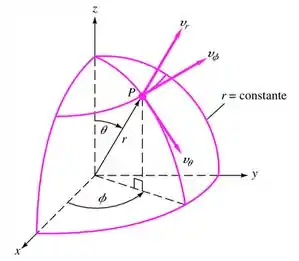
As coordenadas polares esféricas (r, θ, ϕ) são definidas na figura. As transformações cartesianas são

x = r   s e n   θ cos ⁡ ϕ

y = r   s e n   θ sen ⁡ ϕ

z = r   c o s   θ

A relação da continuidade cartesiana incompressível (Equação 1) pode ser transformada na forma polar esférica (Equação 2)

Equação 1

∂ u ∂ x +   ∂ v ∂ y +   ∂ w ∂ z = 0

Equação 2

1 r 2 ∂ ∂ r r 2 v r + 1 r s e n θ ∂ ∂ θ v θ s e n   θ +   1 r s e n θ ∂ ∂ ϕ v ϕ = 0  

Qual é a forma mais geral de v r quando o escoamento é puramente radial, isto é v θ e v ϕ são nulas?

Passo 1

Então chefe, de cara o exercício nos pede pra encontrar v r sabendo que v θ e v φ são iguais a zero.

Aplicando isso na equação da continuidade que ele nos fornece, sumimos com um monte de termos e ficamos com a seguinte expressão:

1 r 2 ∂ ∂ r r 2 v r = 0

Onde chegamos na seguinte conclusão

∂ ∂ r r 2 v r = 0

Se integrarmos a equação acima em r , chegamos na expressão para v r :

v r ( r , θ , φ ) = 1 r 2 C ( θ , φ )

Onde C θ , φ garante a generalidade da solução.

Passo 2

Aplicando a nossa função na equação, sempre teremos a continuidade satisfeita:

1 r 2 ∂ ∂ r r 2 1 r 2 C ( θ , φ ) = 0

1 r 2 ∂ C ( θ , φ ) ∂ r = 0

Como C ( θ , φ ) não depende de r , a derivada será sempre zero.

Resposta

v r ( r , θ , φ ) = 1 r 2 C θ , φ

Exercícios de Livros Relacionados

Uma aproximação útil para a componente x da velocidade em uma camada-limite laminar e incompressível é uma variação parabólica de u = 0 na superfície ( y = 0 ) até a velocidade de corrente livre, U ,
Um campo de escoamento incompressível tem os componentes cilíndricos v θ = C r , v z = K R 2 - r 2 , v r = 0 , em que C e K são constantes e r ≤ R , z ≤ L . Esse escoamento satisfaz a continuidade? O
Dada as componentes das velocidades de dois escoamentos de fluidos incompressíveis: A )v x = x 2 - yv y = x 3 - 2 x y B ) v x = y 3 - 3 x 2 y v y = 3 x y 2 - x 3 Verificar se os dois escoamentos são p
Sendo v x = x 2 + z 2 + 5 ; v y = y 2 + z 2 , determinar a forma mais simples da componente v z que satisfaça a equação da continuidade para um fluido incompressível.
O movimento de fluido incompressível de peso desprezível realiza-se segundo o campo de velocidades v x = a x ; v y = b y ; v z = c z Determinar as condições para as quais o movimento é possívelVerific