Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Equação da Continuidade

Ver Teoria
Exercício 51234678

Enunciado

Um pistão comprime gás em um cilindro movendo-se a uma velocidade constante V, como na figura:

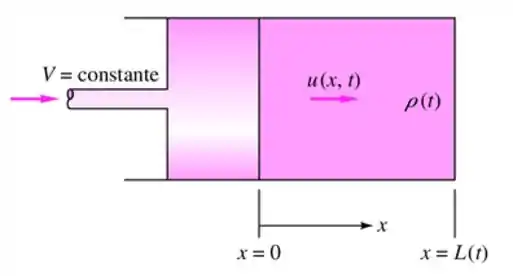
Admita que a massa específica do gás e a posição do pistão em t = 0 sejam ρ 0 e L 0 , respectivamente. Considere que a velocidade do gás varie linearmente de u = V na face do pistão até u = 0 em x   = L . Se a massa específica do gás varia apenas com o tempo, encontre uma expressão para ρ ( t ) .

Passo 1

Então, no enunciado já são dadas diversas informações que serão úteis para a gente nesse problema:

- As condições iniciais do pistão;

- O fato da velocidade variar linearmente ( u = a x + b ):

u 0 = V = b

u L = 0 = a L + V

a = - V L

Logo,

u x , t = - V L x + V

Sendo L a posição do pistão que se move com velocidade constante V ,

L = L t = L o - V t

- A massa específica só varia no tempo.

Passo 2

Olhando a equação da continuidade já podemos eliminar algumas derivadas que simplificarão nosso problema:

∂ ρ ∂ t + ∂ ∂ x ρ u + ∂ ∂ y ρ v + ∂ ∂ z ρ w = 0

d ρ d t + ρ ∂ u ∂ x = 0

Substituindo nossa expressão de u :

d ρ d t + ρ - V L = 0

d ρ d t = ρ V L

Separando as variáveis e integrando:

∫ ρ o ρ d ρ ρ = V ∫ 0 t d t L o - V t

Devemos fazer uma substituição de variáveis x = L o - V t , d x = - V d t

Logo:

d t = - d x V

x 0 = L o

x t = L o - V t

Voltando à equação:

ln ⁡ ρ ρ o = V ∫ L o L o - V t - 1 x d x V

ln ⁡ ρ ρ o = - ∫ L o L o - V t d x x

ln ⁡ ρ ρ o = - ln ⁡ L o - V t L o

ln ⁡ ρ ρ o = ln ⁡ L o L o - V t

Ou:

ρ t = ρ o L o L o - V t

Resposta

ρ t = ρ o L o L o - V t

Exercícios de Livros Relacionados

Uma aproximação útil para a componente x da velocidade em uma camada-limite laminar e incompressível é uma variação parabólica de u = 0 na superfície ( y = 0 ) até a velocidade de corrente livre, U ,
Um campo de escoamento incompressível tem os componentes cilíndricos v θ = C r , v z = K R 2 - r 2 , v r = 0 , em que C e K são constantes e r ≤ R , z ≤ L . Esse escoamento satisfaz a continuidade? O
Dada as componentes das velocidades de dois escoamentos de fluidos incompressíveis: A )v x = x 2 - yv y = x 3 - 2 x y B ) v x = y 3 - 3 x 2 y v y = 3 x y 2 - x 3 Verificar se os dois escoamentos são p
Sendo v x = x 2 + z 2 + 5 ; v y = y 2 + z 2 , determinar a forma mais simples da componente v z que satisfaça a equação da continuidade para um fluido incompressível.
O movimento de fluido incompressível de peso desprezível realiza-se segundo o campo de velocidades v x = a x ; v y = b y ; v z = c z Determinar as condições para as quais o movimento é possívelVerific