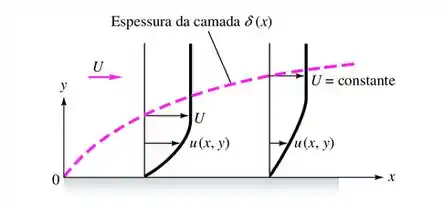
Uma aproximação razoável para a camada-limite laminar incompressível bidimensional sobre a superfície plana da figura é
Admitindo uma condição de não escorregamento na parede, encontre uma expressão para o componente de velocidade para
Depois encontre o valor máximo de em , para o caso particular do escoamento de ar, quando e .
Passo 1
Do enunciado tiramos as seguintes informações:
Por curiosidade, condição de não-escorregamento quer dizer que a velocidade do fluido na parede é a mesma da parede, no caso .
Passo 2
Pare encontramos devemos aplicar a equação da continuidade, para escoamentos incompressíveis e bidimensionais:
Substituindo em :
Calculando a derivada em :
Substituindo na continuidade:
Logo,
Separando as variáveis e integrando:
Logo a resposta da letra a)
Passo 3
Se queremos descobrir o valor máximo de em , devemos usar a relação, para maximizar o valor de ,
Sabemos que:
Conhecemos , e que
De e calculamos :
Substituindo em ,
Temos duas soluções,
Que é onde temos velocidade mínima, na parede.
E,
Que é no topo da camada limite
Logo máximo:
Resposta
Letra a)
Letra b)