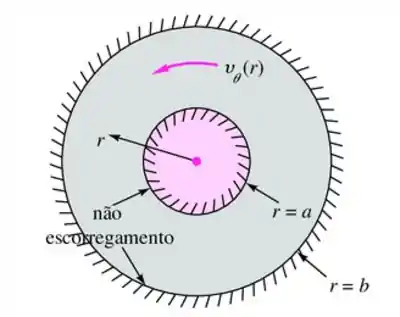
Das equações de Navier-Stokes para escoamento incompressível em coordenadas polares encontre o caso mais geral de movimento puramente circulatório , , para escoamento sem escorregamento entre dois cilindros concêntricos fixos, como na Figura.
Equação da continuidade em coordenadas cilíndricas:
Equações de Navier-Stokes em coordenadas cilíndricas:
Passo 1
Primeiro de tudo já sabemos que só está em função de , e que . Já sabemos daí que a continuidade será satisfeita.
Esses dados simplificarão em muito o problema também. Queremos encontrar o valor da função . Vamos supor que os efeitos gravitacionais não existem.
Passo 2
Da equação de de Navier-Stokes, já aplicando as condições do Passo 1:
Por simetria podemos dizer que não varia com :
Se resolvermos a derivada pela Regra do Produto:
A solução desta equação é:
Passo 3
Se substituirmos as condições de contorno devido ao não escorregamento:
Para também por não-escorregamento:
Supondo que
Se isso for verdade, não haveria escoamento entre os cilindros para satisfazer as condições inciais.
Como o escoamento pode existir, devemos reavliar as hipóteses iniciais. Podemos dizer que o escoamento não existe em estado permanente, ou seja, suas condições variam no tempo o que torna o escoamento muito mais complicado de analisar.
Mas isso não excluiu o fato de existir uma solução geral de escoamentos entre cilindros concêntricos.