Considere a esfera de raio imersa em uma corrente uniforme , como mostra a Figura. De acordo com a teoria, a velocidade do fluido ao longo da linha de corrente é dada por
Encontre a posição da aceleração máxima do fluidod ao longo de e o tempo necessário para que uma partícula de fluido se desloque de a .
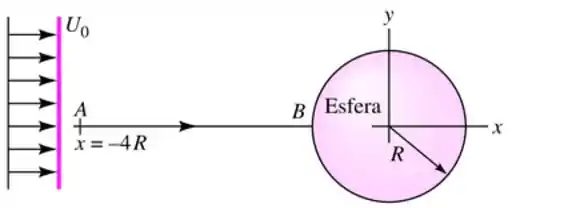
Passo 1
O enunciado nos fornece o campo de velocidade
e nos pede a aceleração máxima ao longo de , antes então devemos encontrar a função que define essa aceleração.
Passo 2
Sabemos que:
Como é um campo unidimensional,
Se,
Temos que:
Substituindo :
Devemos então encontrar o ponto que é máximo, ou seja,
Passo 3
Na letra b) queremos calcular quanto tempo leva para o fluido se movimentar de até .
Sabemos que
Se separarmos a varíáveis ficamos com,
Integrando nos corretos limites de integração:
Tentar resolver esta integral é muito complicado, pois ela não converge para um valor e tende ao infinito. O objetivo da questão era demonstrar que o fluido leva um tempo infinito para chegar ao ponto de estagnação em , onde a velocidade do fluido é zero.
Logo,
Resposta
Letra a)
Letra b)