Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Equações de Navier-Stokes

Ver Teoria
Exercício 12345678

Enunciado

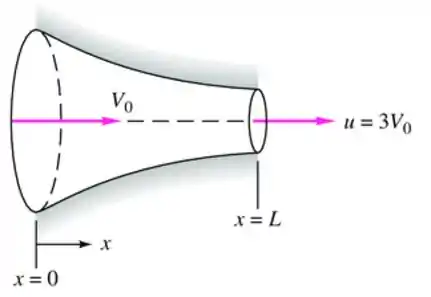
O escoamento pelo bocal convergente da Figura pode ser aproximado por uma distribuição de velocidades unidimensional

u   ≈   V 0 1 +   2 x L ,   v   ≈ 0   ,   w   ≈ 0

a Encontre uma expressão geral para a aceleração do fluido no bocal.

( b )   Para o caso específico V 0 = 3   m / s e L = 150   m m , calcule a aceleração, em g’s, na entrada e na saída.

Passo 1

Esse problema exige de nós lembrar que a aceleração de um fluido é a primeira derivada da velocidade.

Como nosso escoamento é unidimensional, nossa expressão da aceleração se reduz a um termo.

Ao invés de analisarmos isso tudo:

d u d t = ∂ u ∂ t + u ∂ u ∂ x + v ∂ u ∂ y + w ∂ u ∂ z d v d t = ∂ v ∂ t + u ∂ v ∂ x + v ∂ v ∂ y + w ∂ v ∂ z   d w d t = ∂ w ∂ t + u ∂ w ∂ x + v ∂ w ∂ y + w ∂ w ∂ z

É necessário olhar apenas a primeira equação:

d u d t = ∂ u ∂ t + u ∂ u ∂ x + v ∂ u ∂ y + w ∂ u ∂ z

Passo 2

Devemos agora substituir a expressão:

u = V o 1 + 2 x L

Na equação:

d u d t = ∂ u ∂ t + u ∂ u ∂ x + v ∂ u ∂ y + w ∂ u ∂ z

Logo, resolvendo cada derivada:

∂ u ∂ t = 0

u ∂ u ∂ x = V o 1 + 2 x L V o 2 L = 2 V o ² L 1 + 2 x L

v ∂ u ∂ y = 0

w ∂ u ∂ z = 0

Somando tudo, temos a resposta da Letra A:

d u d t = 2 V o ² L 1 + 2 x L

Passo 3

Na letra B ele nos pede para substituir V o = 3   m / s e L = 150   m m = 0,150   m , na expressão que encontramos para a aceleração na entrada x = 0 e na saída x = L = 0,150   m :

d u d t = 2 V o ² L 1 + 2 x L

Na entrada ( x = 0 ):

d u d t = 2 × 3 2 0,150 1 + 2 × 0 0,150

d u d t = 2 × 3 2 0,150 1 + 0

d u d t = 18 0,150

d u d t = 120 m s 2 = 12,2 g

Na saída ( x = L )

d u d t = 2 V o ² L 1 + 2 L L

d u d t = 2 V o ² L 1 + 2

d u d t = 2 × 3 2 0,150 × 3

d u d t = 360 m s 2 = 36,7 g

Sabendo que:

1   g = 9,80665   m / s ²

Resposta

Letra a)

d u d t = 2 V o ² L 1 + 2 x L

Letra b)

d u d t ( x = 0 ) = 120 m / s ² = 12,2 g

d u d t ( x = L ) = 360 m / s ² = 36,7 g

Exercícios de Livros Relacionados

O campo de velocidade para um sorvedouro plano do tipo vórtice é dado por V → = ( - q / 2 π r ) ê r+( K / 2 π r ) ê θ ê ê , em que q = 2 m³/s/m e K = 1 m³/s/m. A massa específica do fluido é 1000 kg/m
Um líquido incompressível com viscosidade desprezível e massa específica ρ = 1250 kg/m3 escoa em regime permanente através de um tubo de 5 m de comprimento com seção convergentedivergente, cuja área v
Para modelar a distribuição de velocidade na seção curva de entrada de um túnel de vento, o raio de curvatura das linhas de corrente é expresso como R = LR0/2y. Em primeira aproximação, considere que
Repita o Exemplo 6.1, porém com uma consideração um pouco mais realista de que o escoamento é similar a um perfil de vórtice livre (irrotacional), Vθ = c/r (em que c é uma constante), como mostrado na
Uma dimensão de uma placa retangular é o dobro da outra dimensão. O ar a uma velocidade uniforme flui paralelo à placa e uma camada limite laminar se forma em ambos os lados da placa. Qual a orientaçã