Dois estudantes desejam medir o diâmetro de um fio de cabelo. Com esse objetivo, realizam um experimento de interferência descrito a seguir. Apoiam uma placa de vidro sobre outra idêntica, ambas transparentes e perfeitamente planas. Colocam entre elas, na extremidade direita de cada placa, o fio de cabelo, como aparece na figura abaixo. Entre as placas, há uma lâmina delgada de ar cuja espessura depende da coordenada horizontal . Por conveniência, a figura está fora de escala.
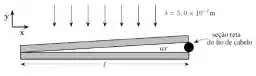
Os estudantes fazem incidir, de cima para baixo, luz monocromática de comprimento de onda de e analisam a interferência dos raios refletidos (de baixo pra cima) em função da posição . Os estudantes verificam que a distância horizontal entre duas franjas escuras é de .
Determine a condição para a interferência CONSTRUTIVA em função da espessura da lâmina delgada de ar.
Sabendo que o comprimento de cada placa é , determine o diâmetro do fio de cabelo.
Passo 1
Letra : Vamos analisar primeiro o fenômeno de interferência de reflexão na imagem abaixo. Esta figura está fora de escala para visualizarmos melhor os raios luminosos.
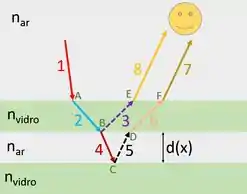
Primeiro, temos o feixe incidindo sobre o vidro no ponto . Parte do feixe é refratado e chamamos de feixe . Logo depois, o feixe incide no ponto do vidro e a parte refletida chamamos de feixe . Já a parte refratada do feixe chamamos de feixe e incide no ponto . O feixe é a reflexão do feixe no ponto . O feixe 6 é a parte refratada do feixe quando o mesmo atinge o ponto . Os feixes 7 e 8 são as partes refratadas dos feixes e , respectivamente. No final, temos o observador recebendo os feixes e interferindo.
A largura é espessura da lâmina de ar entre as placas de vidro a uma distância da extremidade esquerda das placas de vidro. Veja abaixo.
É importante destacar que o vidro tem um índice de refração maior que o do ar, isto é, . Isto será muito importante no passo .
Passo 2
Agora precisamos saber a diferença de caminho ótico dos feixes que chegam no observador.
Note que é do ponto que saem os dois feixes que irão interferir para nosso observador.
O primeiro feixe é o , que é a soma dos feixes e . O segundo feixe é o , pois é composto pelos feixes , , e . É só uma maneira prática de falar.
Agora, se olharmos bem, os caminhos óticos dos feixes , e são iguais. Isto porque eles percorrem as mesmas distâncias (interior da placa de vidro e até o observador).
Isso significa que a diferença de caminho ótico se dá pelos caminhos percorridos pelos feixes 4 e 5! Que maravilha! Como determinamos isso?Como a incidência é quase normal, podemos dizer que, para uma certa distância da extremidade esquerda das placas de vidro, que o feixe percorreu uma distância , enquanto o feixe percorreu a mesma distância . Assim, no total, a diferença de caminho é ! Lembre que a imagem está fora de escala.
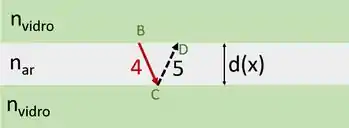
Assim, SOMOS TENTADOS a escrever que a interferência será construtiva se a diferença de caminho ótico for um múltiplo do comprimento de onda da luz no meio, isto é,
e a interferência será destrutiva se a diferença de caminho ótico for um múltiplo ímpar da metade do comprimento de onda, isto é,
com No entanto, estas expressões são válidas SOMENTE se os feixes refletidos mantiveram suas fases! Como a gente verifica isso? Veremos agora no passo 3.
Passo 3
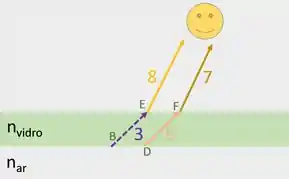
Esta parte é decisiva na resolução do exercício: precisamos saber se os feixes refletidos mantiveram suas fases ou não. Sem saber isso, a gente pode chegar na resposta errada e não queremos isso, não é?Vamos lá! Temos dois feixes que são refletidos: o feixe e o feixe . Eles estão tracejados na figura abaixo
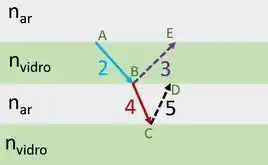
Note que o feixe 3 é a reflexão do feixe 2, este que vai do vidro para o ar (atingindo o ponto ). Já o feixe 5 é a reflexão do feixe , este que vai do ar para o vidro (atingindo o ponto ).Existe uma regrinha muito legal que ajuda a dizer se o feixe refletido mudou de fase ou não (dá pra mostrar essa regrinha usando as equações de Maxwell).

Vamos aplicar essa regrinha.
- O feixe vai do vidro para o ar , então o feixe NÃO MUDA de fase.
- O feixe 4 vai do ar para o vidro , então o feixe 5 MUDA de fase de um valor .
Ih! Deu ruim! O feixe 5 muda de fase!

Vamos entender o que implica nessa mudança de fase.
Quando ocorre uma mudança de fase de valor , na verdade estamos dizendo que o feixe refletido está invertido, como quando vemos uma onda em uma corda atingir sua extremidade, que está fixa em uma parede. Vejam a figura abaixo.
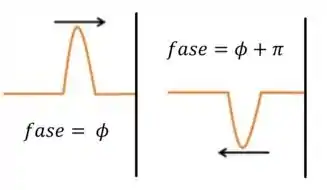
Aí vem a sacada! Um feixe invertido é igual ao feixe original atrasado de !
Desta forma, a equação para “interferência construtiva” que escrevemos no passo 2, a saber,
na verdade, é a equação para interferência destrutiva (pois o feixe está atrasado em )!
E temos também que a equação para “interferência destrutiva” que escrevemos no passo 2, a saber,
é na verdade a equação para interferência construtiva!
Desta forma, podemos escrever que
Passo 4
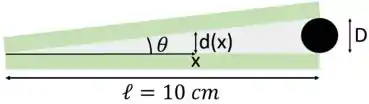
Letra : Primeiro, vamos relacionar a espessura do filme de ar com a posição . Veja a figura abaixo.
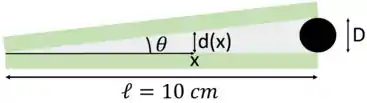
Da figura acima, temos que a tangente de pode ser calculada por
Note também que podemos escrever a mesma tangente da seguinte forma
Assim, igualando as duas expressões, temos que
Podemos escrever as posições que acontecerá uma interferência construtiva. Utilizando a última equação do passo 3 do item temos que
Passo 5
O enunciado disse que a distância entre duas franjas escuras consecutivas é igual a
.
Essa distância é a mesma para duas franjas claras consecutivas. Assim, se as duas franjas claras consecutivas ocorrem nas posições e , então
Utilizando a equação do passo 1 deste item, temos que
Isolando o diâmetro do fio de cabelo, temos que
Substituindo os valores de ; ; e , obtemos que
Resposta