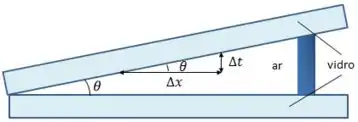
Na Fig.35-46, duas lâminas de microscópio estão em contato em uma das extremidades e separadas na outra.
Quando uma luz com um comprimento de onda de incide verticalmente na lâmina superior, um observador situado acima das lâminas vê uma figura de interferência na qual as franjas escuras estão separadas por uma distância de .
Qual é o ângulo entre as lâminas?
Passo 1
Vamos tentar encontrar a distância entre duas franjas escuras.
A condição para mínimo de interferência é:
Como o filme é ar:
Para a franja escura seguinte, a espessura será:
A diferença de espessuras será:
O enunciado nos diz que , e substituindo:
Passo 2
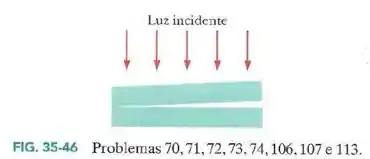
Agora olhemos a geometria do problema:
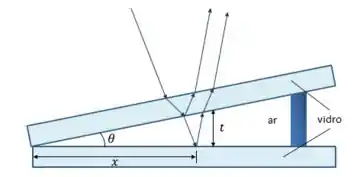
Temos a distância entre duas franjas dadas pelo problema, e a diferença entre as alturas (espessuras), .
Podemos encontrar o ângulo pela sua tangente: